コラム
デジタル社会形成に向けて 第2章(5)~自治体DXの先に~
2022.05.09
前回からの続き
訪問型の行政サービスの効果測定を下記フローに沿って説明してきております。(下図記載)
前回までに、ある訪問型行政サービス(A公園の訪問価値)について、得られたデータを散布図に図化し、それが経済学入門でも紹介される「需要曲線」であることを紹介いたしました。
今回は、得られたデータを元に「価値計算の方法」に話しを進めます。
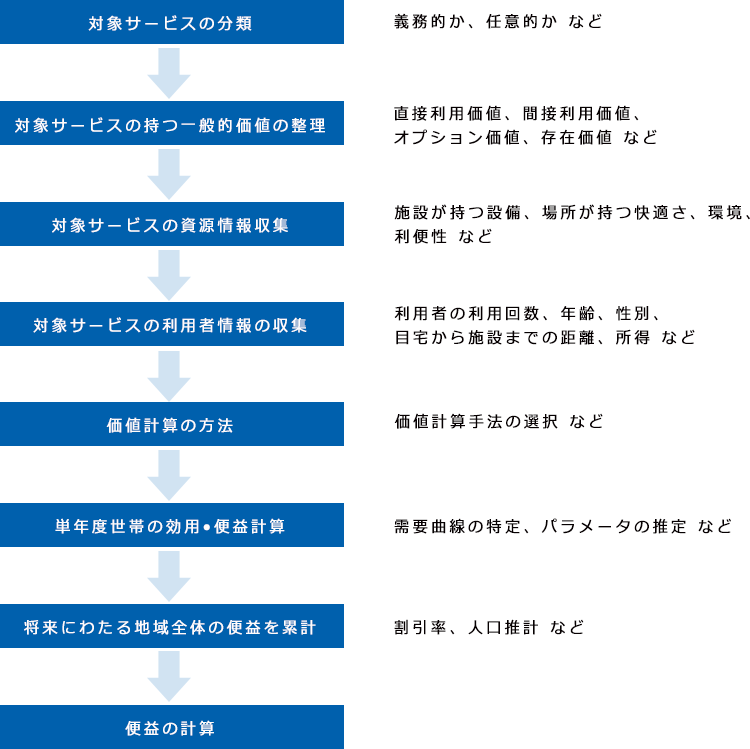 図:訪問型行政サービスにおける効果測定フロー
図:訪問型行政サービスにおける効果測定フロー
訪問型サービスの価値は「機会費用」で
タイトルのとおり、結論は至極単純でした。おさらいしますと、すなわち、訪問型サービスについては、まず、そのサービスが選択されたという事実が重要です。そして、それは訪問人数(回数)によって表す事が出来ます。あるいは、計測出来るならば、「のべ滞在時間」などの情報も欲しいところです。
次に、価値の測定方法はどうするか?これは主として機会費用を使うことになります。機会費用というのは、ある一定時間を他の事に使えば得られるかもしれない未実現利益のことです。例えば、面白くない映画であっても、勿体ないとの理由から最後まで視聴し続けた場合の機会費用は、「チケット代+時間コスト」になります。仮に120分の上映時間で、チケット代が1,800円、1時間あたりの時間コストを1,200円とした場合、1,800円+(1,200円 × 2時間)と算出できます。上映開始後のチケット代の払い戻しは難しいため、埋没費用(※1)として諦めるが潔しです。サッと席を立ちましょう。時間コストは回収できますので。
右下がりの線は何だったのか?
前回のコラムにおいて、「三角形の面積によって、ある訪問型サービスの価値を近似的に表現出来ているのではないか?」という件についてですが、内容を簡単にするために、いくつか省略した箇所があります。
1つ目は、「訪問回数(人数)と移動費用(距離)の関係は線形(比例関係)なのか?」という点です。前回提示したグラフを見ていただくと、右下がりの直線になっており、実際に観測された点の間を縫う様に、良い感じで線が引かれているのが分かります。いわゆる回帰直線と言われる、残差平方和が最小になる様な直線が選ばれております。
観測点の中に直線を引く場合、直線の候補は無限にある訳です。その中の一本を選ぶには、ある基準が必要となるため、取り敢えず、その線と各観測点との乖離幅(残差)の二乗の合計が最小になるような線を選んでみることになります。
二乗の総和を最小にするために、最小二乗法(※2)という手法が採用されております。観測されたデータを、一本の直線で表現するためには、残差平方和を最小化する以外に、絶対値を最小化するという手法(最小絶対値法)もありますが、難解であるため割愛させていただきます。
直線で表記されていなくても、曲線で表記しても問題ありません。例えば、同じデータを使って、表計算ソフトでグラフ描画時に設定を調整すると下記のような結果になります。
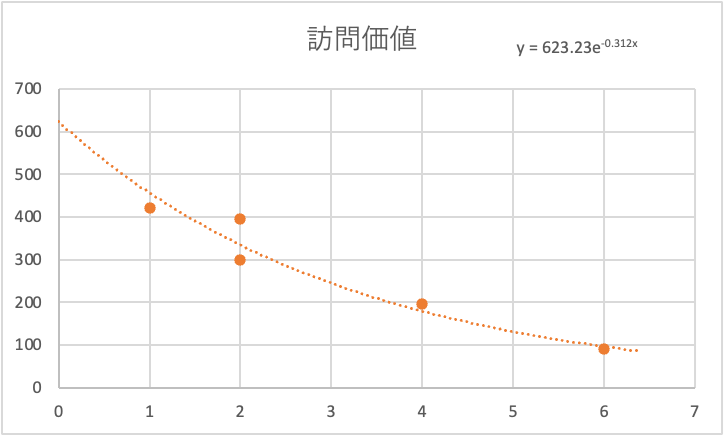 図:散布図(その2) A公園の訪問価値
図:散布図(その2) A公園の訪問価値
表計算ソフトが自動で関係式を表示してくれます。この例では、訪問人数(横軸)と費用(縦軸)の関係が、曲線で表現されており、具体的には指数関数の関係になっており、直線ではなく曲線でも表現される事が分かります。
では、直線なのか?曲線なのか?その決め手はいったい何なのかということなのですが、その1つとして「当てはまりの良さ」が挙げられます。言い方を変えれば「説明力」です。そうなると、次は説明力を測る物差しを用意する必要が生じます。統計に精通していらっしゃる方であれば、「決定係数」というものが存在することをご存知でしょう。ただ、非線形回帰の場合は、決定係数の定義そのものに様々な意見があるため、楽にお話出来なくなります。
そもそも、直線か曲線かといった話をする前に、訪問人数と訪問費用という2つの変数の関係だけを論じるのでは足りなくて、他に多数の要因が絡まっているのではないのか?という問題もあります。回帰分析でいうと、複数の要因が一つの結果を説明している場合、つまり重回帰分析です。ある事象間の関係を記述することは、その分野や目的に依存して決まる要因も多いため、絶対というのは無さそうです。
例えば、医療分野において、ある投薬の効果が時間の経過を経て、どのような効用をもたらすか?といった時の経過を盛り込んで事象を記述したい場合には、やはり非線形(曲線)で記述せざるを得ないでしょう。他方で、今回の事例の場合は、単回帰で良いかどうかは別として、短期的に考えた場合、とりあえず時間概念は捨象しても差し支えないため直線で表記いたします。
また、非線形で記述した場合は、解釈が若干難しくなる傾向があります。曲線の場合、ある地点での政策効果を測るためには微分が必要になり、全体の政策効果、すなわち、面積を出す際にも積分が必要になります。線形(直線)で記述した場合は、線のどこでも傾きは一定であるため、どこで測っても効果は一定と見做せます。(正しくは見做している、ということになりますが。) 全体の面積計算も三角形ですから簡単です。この続きは次回以降に。(つづく)
コラムニスト
公共事業本部 ソリューションストラテジスト 松村 俊英
参考
- ※1sunk cost 事業や行為に投下した資金・労力のうち、事業や行為の撤退・縮小・中止をしても戻って来ない資金や労力のこと。
- ※2観測値と予測値の誤差の二乗和が最小になるように決める方法
https://bellcurve.jp/statistics/glossary/1809.html
関連コラム
- デジタル社会形成に向けて 第2章(1)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(2)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(3)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(4)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(5)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(6)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(7)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(8)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(9)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(10)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(11)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(12)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(13)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(14)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(15)~自治体DXの先に~
- 「データ分析を考える」コラム一覧に戻る
