コラム
ゲーム理論で俯瞰する公的部門の問題②「仕組み(ルール)作りと人の行動」
2016.05.18
ジャパンシステム株式会社 コンサルティングアドバイザー
首都大学東京 客員研究員 河重隆一郎
今回は、仕組み(ルール)によって人の行動がどのように変化するのかについてゲーム理論を用いて考えてみたい。
ゲーム理論は2人以上のプレイヤーの意思決定を分析する理論である。意思決定の方法にはゲーム理論のほかに概ね2つの方法がある。ひとつは統計的問題や技術的問題を解くことである。これらの手法を用いた分析や最適化を行なうことを工学や理学は目的としている。なかでも制御工学と呼ばれる自動制御の理論が社会にもたらした影響は計り知れないほど大きい。航空機の自動操縦から家庭のマイコン電子ジャーまで自動制御の技術なしでは、現代社会は一日たりとも立ち行かないだろう。
ふたつ目は市場による消費と生産の決定である。確かに、共同体の論理では不可能なほど大規模な不特定多数の個人による互助システムが、市場の論理によって勝手に立ち上がる。しかも、そのシステムの立ち上げに必要なものは、個人のインセンティブとお金を介した取引を行う無数の市場だけなのである。この原稿を書くために使っているPCの部品や動作に必要な電気を作ってくれるのは顔見知りの人ではない。
多くのゲーム理論の入門書では、ゲーム理論の概要解説に続いて、ゲームの定式化として本稿で前回示したゲームの木や利得行列(payoff matrix)と呼ばれている利得の早見表の書き方と読み方を教えるのが定石である。そして「囚人のジレンマ」とか「コイン合わせ」とか「両性の戦い」というような有名なゲームが登場して、その解き方を教えてくれる。なかには開拓時代の西部劇の酒場を彷彿とさせるドラマ仕立てもある([1] Cho and Kreps, 1987)。
これは、対象となる問題のイメージを大まかにつかむために先人達が工夫した結果なのであろう。子供の頃習った「つるかめ算」や「植木算」などのような算法の命名法と似ていると筆者は思う。
こうした入門書の読者の大方は、なるほどそういうものかと感心したり納得したりするであろう。その一方で、現実の意思決定や問題解決に直面して何とかしなければならない読者にとっては、囚人の自白やオペラへ行くか野球観戦するのかでもめている男女の話を知ったところで、現実問題にどのように応用して良いのか解らないという声を聞くことは、そう珍しいことでは無い。公共部門の問題に携わる読者の皆さんも同様の印象をもたれる方はおられると思う。
前回のソフトな予算制約の問題においてもそうであるように、合理的な個人による市場競争と政府による統制・介入とによる二元的な図式で、現代の経済学は社会を特徴づけてきた。わが国でも公か民かという議論を繰り返している。しかも、市場(民)の共同体(公)に対する優位性が極端に誇張された感情論が支配的で、形勢は共同体に分が悪いように見える。
しかしながら、市場の失敗と経済学で呼ばれている欠陥が市場システムにはある。むしろ、個人による自己利益の追求が社会全体の利益の最大化を達成するという考え方は、競争市場では成り立つものの、一般的な社会や経済ではそれが成り立たないほうが普通である。社会問題の解決には当事者どうしの意見の対立を調整することが求められる。
さて、ある地方の市が旧市街にある商店街の活性化計画として「歩いて楽しいまちづくり」というコンセプトのもと、駐車場の整備を行う例を考えてみよう。駐車場ができたならば、商店街の全員が程度の差こそあれ何らかの便益を受けることはわかっている。しかし市の予算だけでは資金が不足するために、商店街の組合が地元の銀行から融資をうけて不足分を賄うことにした。駐車場によって受ける便益の大きさにしたがって、組合に加盟している各商店が借入金の返済を月々負担するものとする。
いま、代表的な二つの商店AとBについてゲームの定式化をしよう。どちらの商店も駐車場建設に「賛成」と「反対」の2つの行動を選ぶことができるとする。 A・Bともに駐車場のおかげで毎月8万円の利益増が見込めるという見積もりが出ている。
両者がともに建設に賛成ならば、各商店の負担額は毎月5万円で、 どちらか一方のみが建設に賛成ならば, 賛成した商店が毎月10万円負担することで駐車場はできあがるとしよう。
このときの利得の早見表(利得行列)を表1にしめす。カッコ内の左側が商店Aの利得で右側が商店Bの利得である。
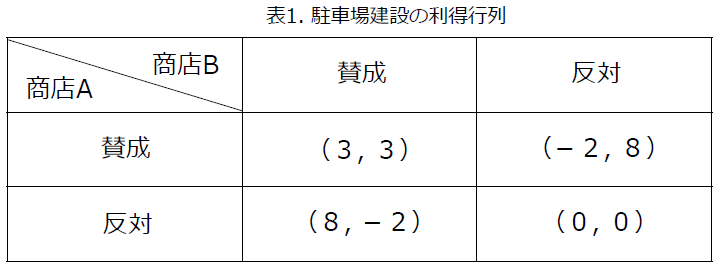
A・Bともに反対したときには駐車場ができないために、毎月の利益は増えないのでA・Bとも利得は0円になる(表1の右下欄)。いま、Aが建設に反対したときにBが賛成して駐車場ができてしまえば、Aは費用負担なしで駐車場の便益8万円を得ることができるが、Bは2万円の損失が出る(表1の左下欄)。
つまり、共に賛成すれば毎月3万円の利益を得られるのだが(表1の左上欄)、 このとき自分だけ反対すれば8万円の利益を得ることができる。ここで注目すべきことは, 相手が反対しているときにも自分は反対したほうが良いということである。
結局、両方とも反対をするために駐車場の計画は中止になってしまう。これは一般に公共財のフリーライド(ただ乗り)問題と呼ばれているが、実はこのゲームは「囚人のジレンマ」と同じ形式なのである。
このゲームの結果を見るかぎり、合理的な個人の自由に任せることで効率性が実現できるという考え方は正しいとは言えない。つまり合理的な個人が交渉を通じてより良い結果にたどり着くという「コースの定理」の主張には見落としがあるのである。このように、個人の合理性と社会全体の合理性とが相容れないことを囚人のジレンマが明らかにしたといえる。
ここでは問題を単純化するために便益がどちらも8万円と解っているとしている。しかし実際は、各商店が自分の便益については予測可能である一方、他の商店の便益については良く解らないというのが一般的であろう。
このとき各商店の自己申告によって便益を決定するならば、費用の配分は便益にしたがって行うことになっているから、各商店ともに自分の便益を過小に申告すると得をすることがわかっている。このように費用負担を公正に決定することすら困難を極める。実は、この正しい便益を申告するか否かという行動も囚人のジレンマになっていると考えることができるのだ。このような問題があるために、計量的な手法による費用便益分析が公共事業の決定にあたって義務付けられていると考えることができる。
費用・税の負担や入札などのような問題は、仕組み(ルール)が変わるとそれに合わせて人は自分に有利なように行動を変化させる。したがって、住民が「反対」あるいは「賛成」しているからといって、その結果を素直に受け入れて公共財への投資を決定するのではなく、どのような仕組みにしたがって住民たちが意思決定をしたかを読み込んで、仕組みを設計する能力が公的組織には求められるのである。このときゲーム理論は大変強力なツールとなる。ゲーム理論による仕組みや制度設計の理論はメカニズムデザイン(mechanism design)と呼ばれ、入札方法・投票ルール・契約方法などの設計に用いられている。メカニズムデザインの考え方は現代の経済学でもっとも重要な分野の一つと言えるだろう。今回は紙幅の関係でこれにとどめるが、回をあらためてメカニズムデザインの具体的な例について説明する予定である。
[参考文献]
[1] Cho and Kreps(1987). ” Signaling games and stable equilibria”, The Quarterly Journal of Economics, pp. 179-221.
[2] 渡辺隆裕(2008), 「ゼミナール ゲーム理論入門」, 日本経済新聞出版社
