コラム

デジタル社会形成に向けて　第2章（16）～自治体DXの先に～

2023.06.05

訪問型行政サービスの効果測定を下記フローに沿って説明してきております。（下図記載）

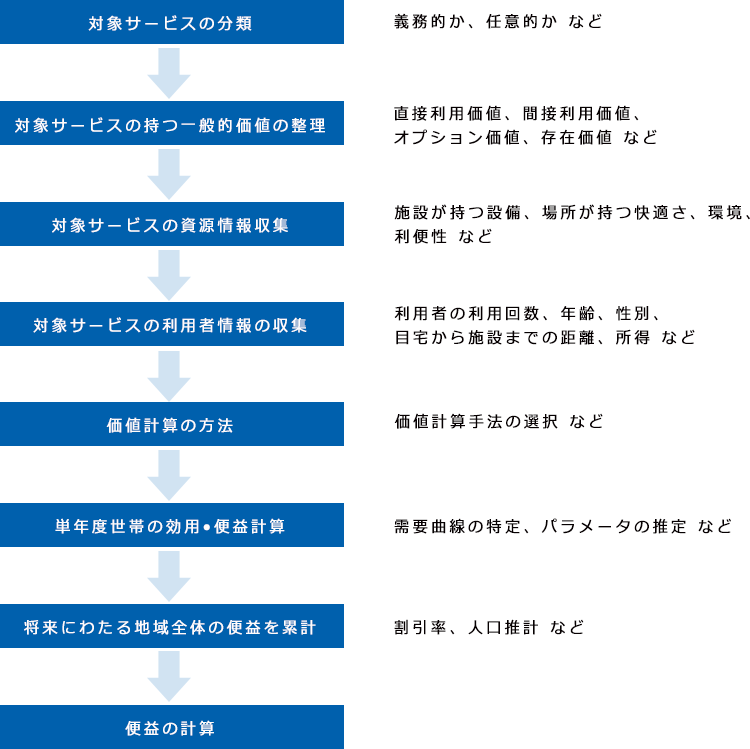図1：訪問型行政サービスにおける効果測定フロー

前回からの続き

前回までのコラムで回帰分析のおさらいをしておりました。何でそんなことをやっていたか？と申しますと、公共サービスの利用者が、ある施設やサービスを「利用する／利用しない」という意思決定の結果について、その利用者の属性やサービス等の属性情報から説明できないか？ということでした。

例えば、市民の方に対して「普段、どこの公園（公共サービス）を利用しておりますか？その目的は？」といったアンケートを実施したとしましょう。その際に、住所・年齢・性別・家族構成。更に可能であれば職業・年収なども聞ければ理想です。アンケートの回答として「○○公園（公共サービス）を利用している、あるいは利用していない」という結果を入手できたら、それぞれの公園の属性を調べます。住所・規模・設備などです。これらの利用者情報／設備情報の組み合わせから、果たして、yes/noという回答を上手く説明できるか？という訳です。

仮に、いくつかの情報によって上手く、利用者の意思決定を説明できたならば、これは政策の意思決定上、有益な情報になるでしょう。仮に、公園利用を促進することが政策目標として決まっているのであれば、公園設備を充実させるべきなのか？広さが重要なのか？最も公園利用に影響力のある事項に対して、重点的に投資を行えば良いということになります。

勿論、この類の情報は普段からアンケート等で収集できているかもしれませんが、我々の狙いは、市民向けアンケートから「定量的な効果」を測定できないだろうか？という所にあります。

では、いよいよこの「yes/no」を上手く説明できるモデルを考える段階に至りました。回帰分析で良いのでは？と思われるかもしれませんが、説明される側の変数（目的変数）が「yes/no」の2つの値(二値)しか取らない場合、通常の回帰分析では上手く説明できません。そのため、少々強引ですが、下グラフをご覧下さい。

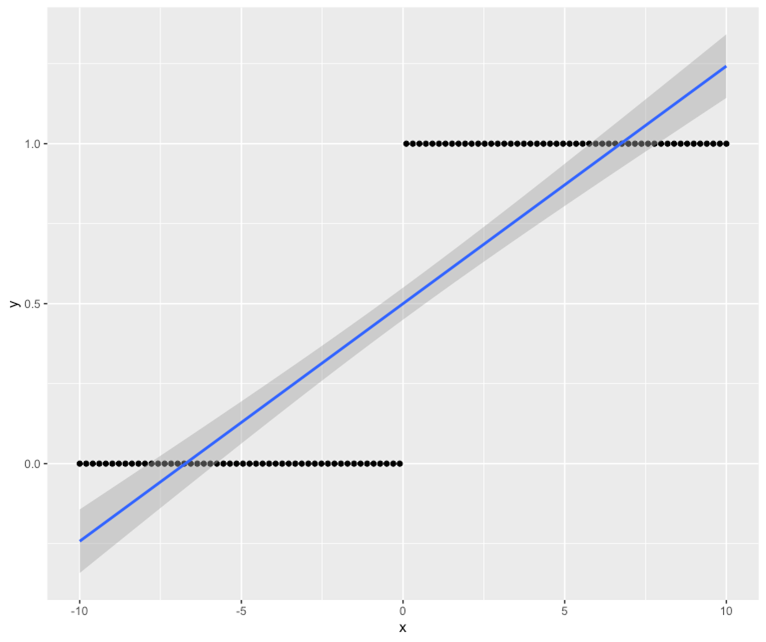図2：グラフ（回帰分析結果）

まず、ｘの値として−10から10まで等間隔に並ぶデータを100個用意し、その上で0以下ならばｙ＝0、0以上ならばｙ＝1となるｙとｘのデータセットを作りました。グラフは、そのようにして作ったｙをｘで、回帰分析したものです。当然ながら線型で回帰すると、右上がりの直線が引かれます。この状況では、0と1に分かれて存在するｙの各点を、上手くｘとの関係で表現しているとは言い難いでしょう。

そのため、通常の回帰分析によって、すなわち、線型で表現する事を諦めて、何か一手間加えて、上手く0と1に分かれて存在する各点を繋いで表現しうる方法はないか？と模索する必要が生じます。

ロジスティック回帰分析

ここで登場するのがロジスティック回帰分析という手法になります。ロジスティック回帰分析は、被説明変数（目的変数）yが二値を取り、説明変数xが1つ(単回帰)、あるいは複数(重回帰)ある場合に、yをｘで説明するための分析手法です。上記グラフの通り、通常の線形回帰モデルにおいて、ｙを0か1、あるいは、0〜1の間の数値しか出力しないような制限を設けることはできません。そのため、ロジスティック回帰を用いて、線形回帰の出力ｙを0～1の間の値に変換する処理を施して、線形回帰を拡張する方向性に進みます。

下図をご覧下さい。右上がりの直線に加えて、S字が間延びした様な曲線が描かれています。これが、ロジスティック回帰といわれるものになります。

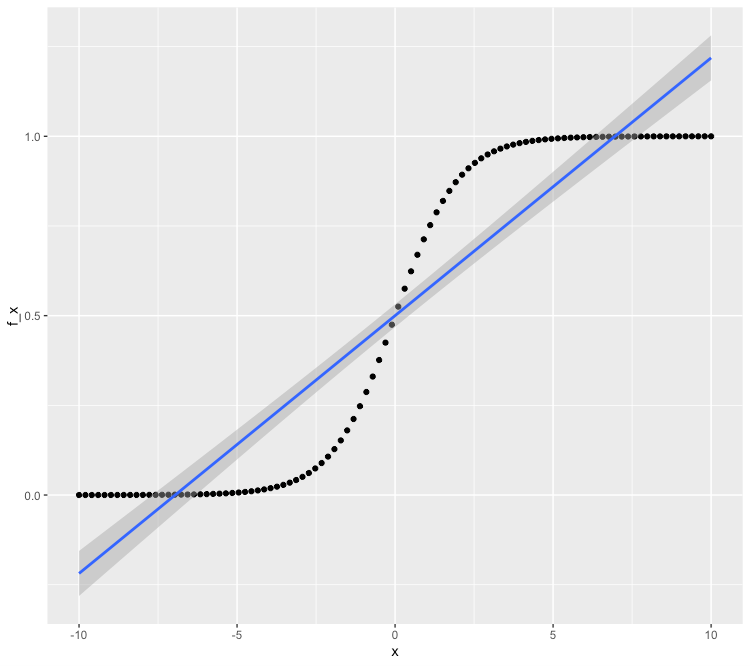図3：グラフ（ロジスティック回帰分析結果）

ｘ軸(説明変数がｘ一つ)を左から目で追っていくと、0の手前くらいまで、ｙは0近傍に張り付いております。ところが、0の手前、マイナス2.5くらいまで来ると、急激にｙの値が大きくなって、1を目指して大きくなります。この例では、ちょうど、ｘ＝0のところで、ｙは0.5になっております。その後、ｙの値は、ｘ＝0を過ぎてプラス2.5辺りから、今度は1の辺りにｙの値が張り付いて、その後水平に近い感じで伸びて行きます。

この曲線の形状がとっても好都合です。直線は連続しておりまして(切れ目がない)、ｘ＝0の近傍 (ｘ＝-2.5〜ｘ＝2.5)で、ｙが0でもなく、また、1でもない領域が出現しておりますが、それ以外のｘでは、ｙは潔く、0か1になっております。言い換えると、「1＝サービスを利用する」、「0＝サービスを利用しない」、とした場合、ｘ（施設の設備充実度)が-2.5くらいまでは、ｙ＝0ですから、施設は利用されない。他方で、ｘが2.5を超えてくると、その施設・サービスは利用される、と読めそうです。ｘ＝0の近傍 (ｘ＝-2.5〜ｘ＝2.5)は、ちょっと微妙な感じです。0でもなく、1でもないということなので、どちらに転ぶか分からない領域と言えます。

このように、線形回帰モデルの出力を0～1の間に変換するために、ロジスティック関数が使われます。ロジスティックとは、主に「兵站・物流」の意味で用いられますが、この場合ですと「記号論理学」の意味合いが含まれているようです。

なお、ロジスティック関数は、以下のような計算式で表せます。
Y = 1 / (1 + exp(-1 * x))
少々見慣れない記号なども登場しておりますが、その辺は次回以降に。

（以上）

コラムニスト
公共事業本部　ソリューションストラテジスト　松村　俊英

デジタル社会形成に向けて 第2章（16）～自治体DXの先に～

前回からの続き

ロジスティック回帰分析

関連コラム

デジタル社会形成に向けて　第2章（16）～自治体DXの先に～