コラム

  1. HOME
  2. コラム
  3. データ分析
  4. デジタル社会形成に向けて　第2章（17）～自治体DXの先に～

デジタル社会形成に向けて　第2章（17）～自治体DXの先に～

2023.07.10

訪問型行政サービスの効果測定を下記フローに沿って説明してきております。（下図記載）

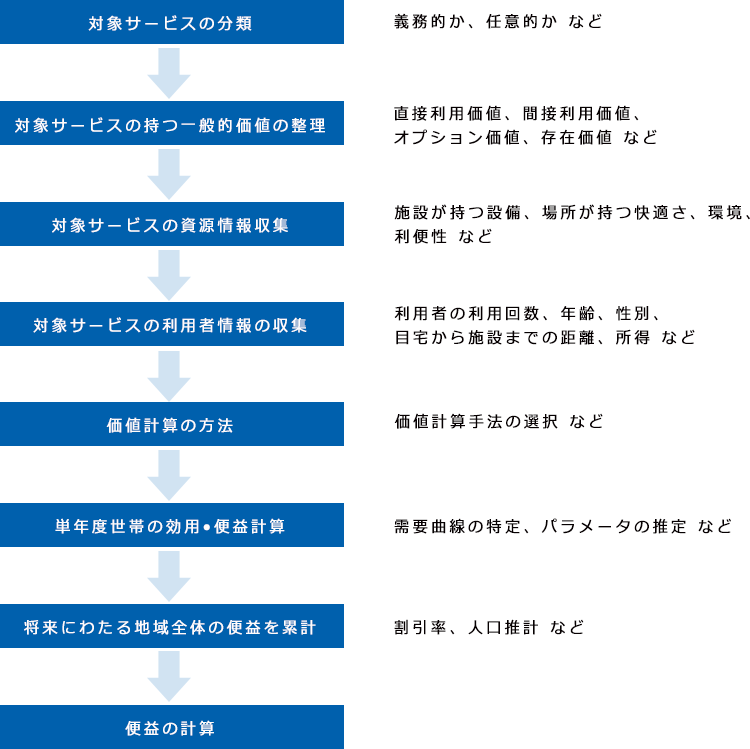訪問型行政サービスにおける効果測定フロー図1：訪問型行政サービスにおける効果測定フロー

前回からの続き

前回までのコラムで、「0/1」「買う／買わない」「行く／行かない」といった確率的なイベントが、何らかの複合的な要因で決まるモデルを追求した結果、ロジスティック関数と呼ばれる関数によって、上手く表現できそうだというお話をしました。贅言※1ながら、我々の日常は、何かを「する／しない」の選択を、意識的にせよ、無意識にせよ、絶え間なく繰り返しながら流れていると言えましょう。

正規分布のおさらい

それはさて置き、直線による回帰分析でも同様でしたが、説明したい事象（今は「0／1」のどちらかを取るケースです）が、確率的な現象であると考えると、色々な統計ツールが使えるので便利です。そして、確率的な現象であると考えられるならば、それには何らかの「分布」が存在するはずです。一般的には「正規分布」が有名ではないでしょうか？通常、線形回帰を行う際には、その背後に攪乱項（かくらんこう）の正規分布を想定しているかと思います。

正規分布の場合、どんな塩梅で分布するかといいますと、グラフ集計など様々な場面でお目に掛かる下記図２の分布です。左右対称になっており、釣り鐘の様な形をしております。この例では、釣り鐘の頂点といいますか、山頂部分が丁度0になります。無理矢理０にする必要もないのですが、たまたま、このように平均が0で、標準偏差(＝分散)が１の正規分布は、特に標準正規分布と呼ばれ、多くの統計で用いられています。

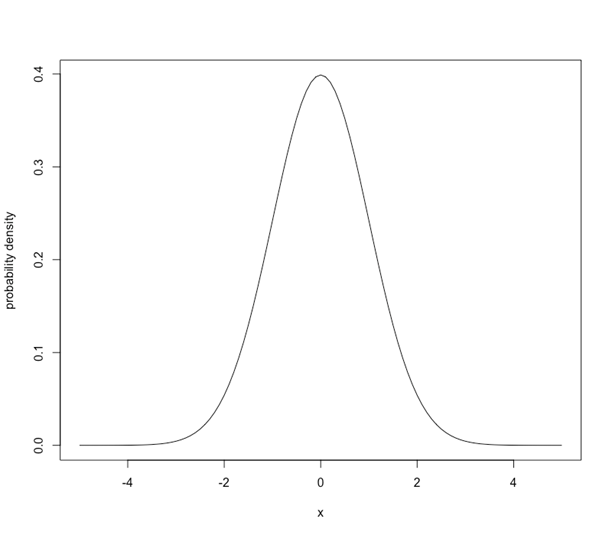図2：標準正規分布 図2：標準正規分布

この釣り鐘状の図形が何を意味しているのか？ご存じの方も多いと思いますが、ある事柄の「分布」、つまり、「度数」を並べたものになっています。

それを理解していただくためには、ある物事が発生した回数を順番に積み上げていった結果（下記図３）の「ヒストグラム」が最適です。左端から発生回数を足し算していきながら、右端まで全部足し上げると、全体の発生回数が解ります。この例では14のブロックに分かれていますが、例えば、一番左端の僅かに発生している部分の発生確率は？と問われれば、その部分の発生個数を全体の個数で割ってやれば、計算できます。

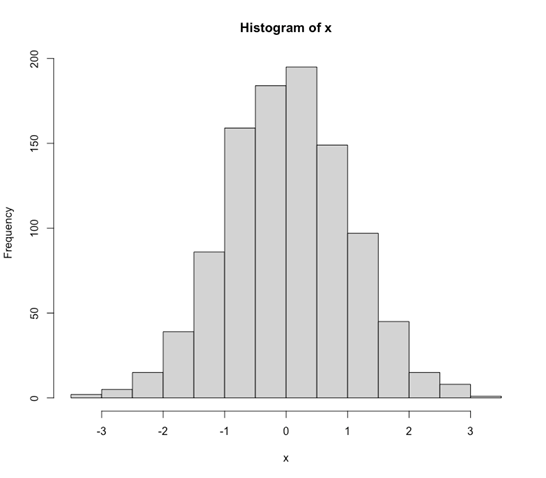図3：ヒストグラム 図3：ヒストグラム

ということで、このヒストグラムのブロックを細分化していくと、上記図1の（標準）正規分布に近づいていきます。（下記図４を参照）

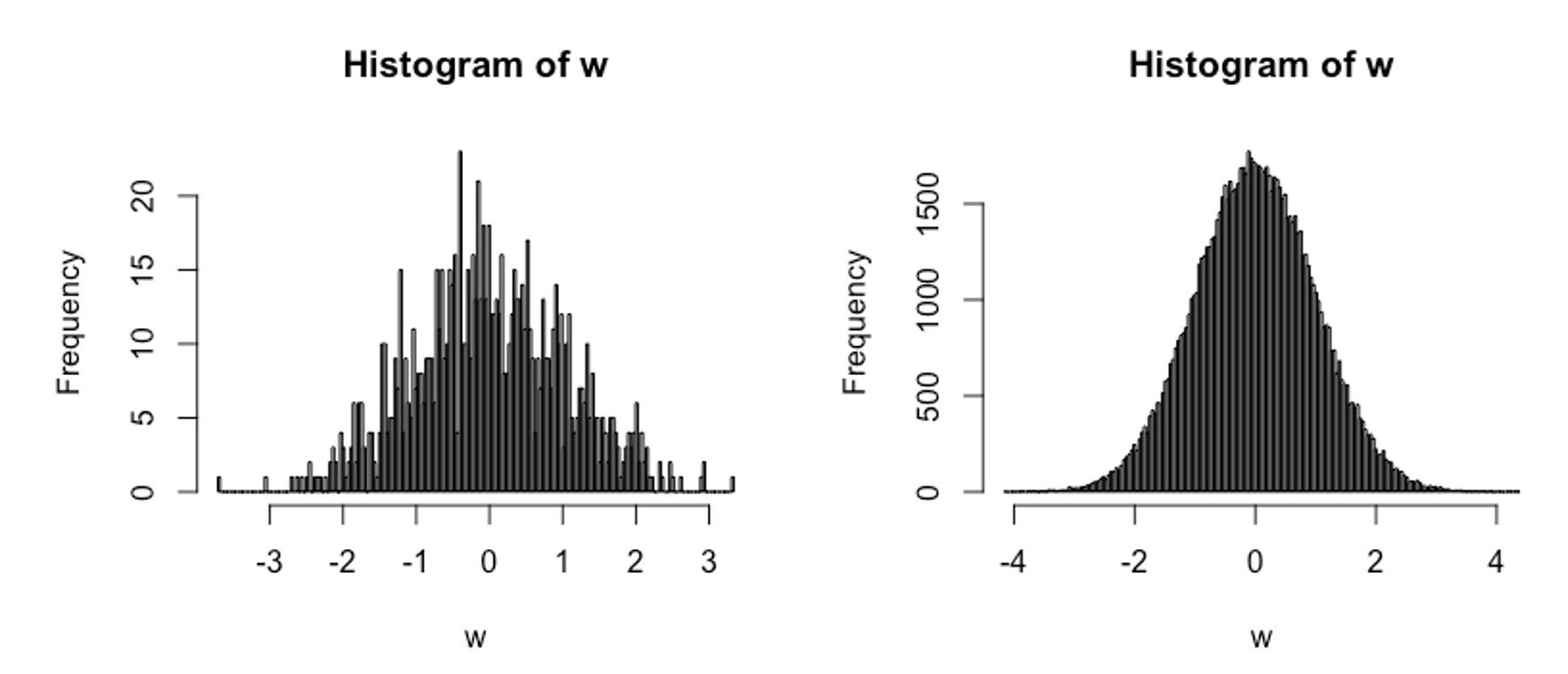図4：ヒストグラム（細分化した結果） 図4：ヒストグラム（細分化した結果）

したがって、正規分布の場合も、ある場所での発生確率は？と問われれば、計算する事は可能です。ただ、ヒストグラムでは存在したブロックが潰れてしまい、線形になってしまっているため、残念ながら単純にカウントすることはできません。そこで「積分」を用いて計算することになりますが、兎も角、必要な区間の面積が計算できるため、結果として、「ある区間の面積／全体の面積」という計算式で、確率計算が可能になる訳です。全体の面積は「1」です。

正規分布をカウントしていく

さて、標準正規分布は、中央部、すなわち平均「0」の部分が山頂になっておりますが、ここの度数＝個数が最も大きくなっております。他方で、左端や右端は小さくなります。平均から遠ざかると、発生事象＝個数が少なくなるのですね。ここで、左端から個数を数え上げて、順番に足し上げて行くことを考えてみて下さい。実際には面積を計算することになりますが、兎も角、山の頂の所で左右対称になるため丁度、面積＝確率は半分になります。山の頂点から右に行くと、面積は増えていく反面、その増え方は徐々に小さくなり、右端に近づくと、ほとんど増えなくなってしまいます。そのような面積の増え方を示したものが下記の関数（図５）になります。

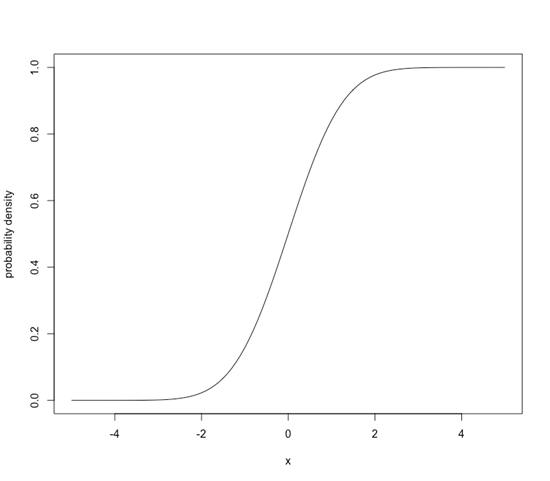図5：標準正規分布の累積分布関数" 図5：標準正規分布の累積分布関数

この形は！と気付かれた方もいらっしゃいますが、前回のコラムで紹介したロジスティック回帰の形です。丁度中心の０を挟んで、左は0近傍に線が張り付いており、中心から右側では1近傍に線が張り付いております。「0か1か」「行くか行かないか」といった、被説明変数が二値をとる問題を考える際に、このような形状になるのが好ましいです。

正規分布とロジスティック分布

ロジスティック分布（図６）は、正規分布と比べると、心持ち平べったい感じになっています。その結果、その累積分布関数（図７）も、正規分布のそれに比べて、チョッと緩い感じになっています。

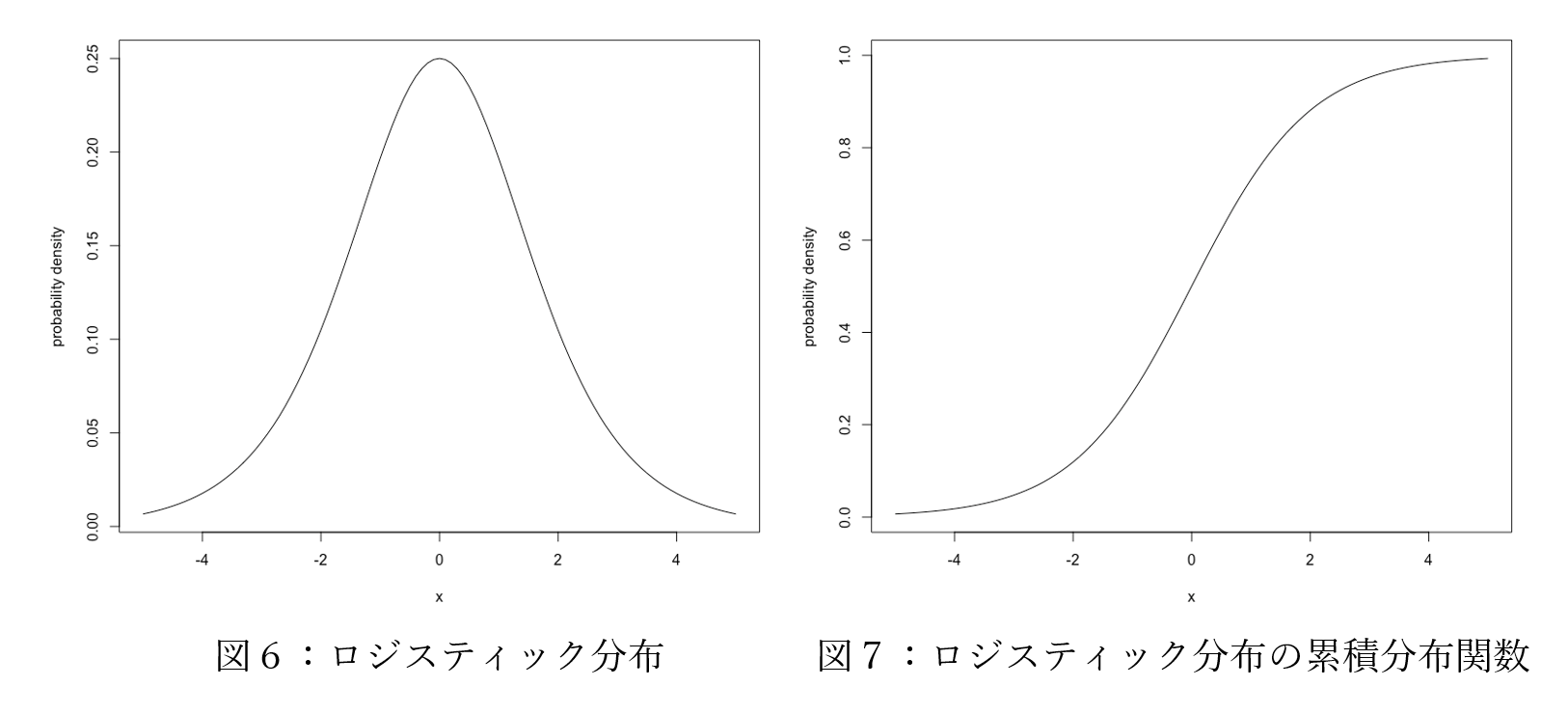
図6：ロジスティック分布

こうしてみると、二値問題を扱う際には、ロジスティック分布よりも、正規分布を想定した方が良さそうにも見えます。実際に、(標準)正規分布から始めて、累積分布関数を求める手順は「プロビット変換」として知られていて、様々な分析で用いられています。

「ロジスティック分布と正規分布のどちらが良いのか？」という問題については、本稿の範囲を超えておりますが、私の見解としては、線形回帰からの応用として、正規分布を前提にした方(プロビット変換)が、分かりやすいような気がします。

(以上)

コラムニスト
公共事業本部　ソリューションストラテジスト　松村　俊英

※1　贅言（ぜいげん）／あえて言わなくてもいい言葉のこと

関連コラム

カテゴリー一覧へ戻る