コラム

  1. HOME
  2. コラム
  3. データ分析
  4. デジタル社会形成に向けて　第2章（12）～自治体DXの先に～

デジタル社会形成に向けて　第2章（12）～自治体DXの先に～

2023.01.10

訪問型行政サービスの効果測定を下記フローに沿って説明してきております。（下図記載）

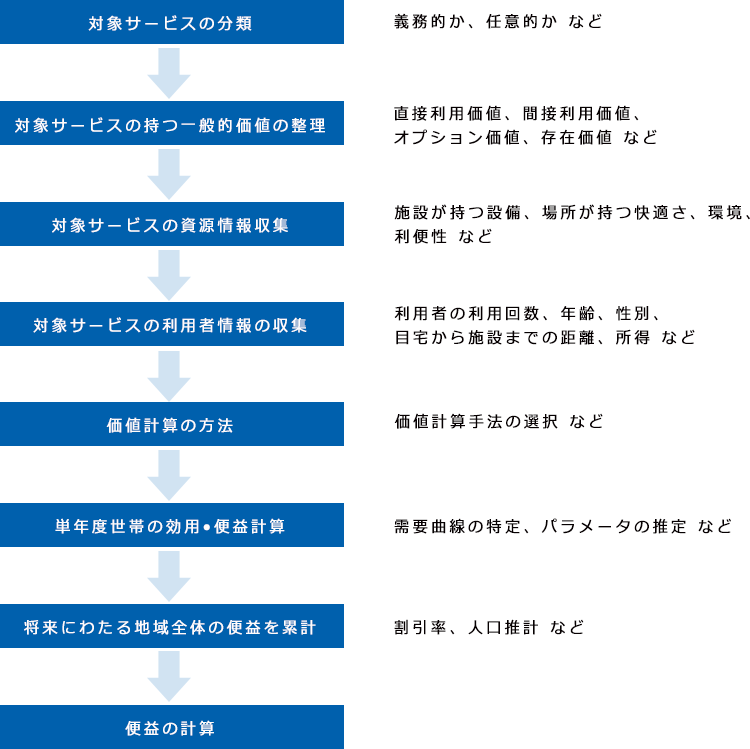訪問型行政サービスにおける効果測定フロー図1：訪問型行政サービスにおける効果測定フロー

前回からの続き～相関係数について

前回コラムより、「相関とは何か？」という話をしております。2つの事柄について、「関係がある」という状態を、統計上の用語である「相関」と、その（直線的な）絡まり具合を数値化した「相関係数」で説明しようとしています。相関係数は、以下の数式で計算されます。本来は、共分散も標準偏差も平均を取りますが、分子／分母で相殺されるため、省略しています。

分子：変数ｘと変数ｙの共分散（＝偏差の積和）
分母：変数ｘと変数ｙの、それぞれの標準偏差の積
分子／分母を求める

相関係数の分子

分子のイメージを下記表1に図解します。まず初めに、変数ｘと変数ｙについてそれぞれ平均からの差分を計算します（偏差）。次に、変数ｘの偏差と変数ｙの偏差を掛け合わせて個数分の四角形を作ります。最後に、それら四角形の平均を取ります。実際のところ、偏差にはマイナスもプラスもあるため、変数ｘ、変数ｙの偏差の組合せが「＋×＋」や「－×－」の場合、四角形はプラスの面積になりますが、「－×＋」や「＋×－」の場合、マイナスの面積になります。このようなプラスとマイナスの面積を足し合わせますので、マイナスの面積が大きければ、分子はマイナスにもなります。

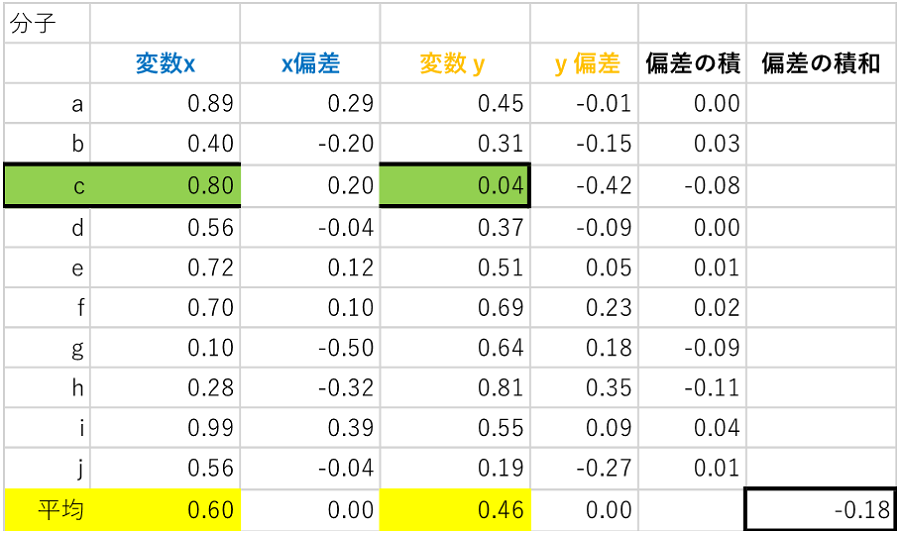相関係数（偏差の積和）表1：相関係数（偏差の積和）

計算した結果、上記数値例でも偏差の積和はマイナスになっております。
変数ｘ、変数ｙの偏差の組合せが「－×－」や「＋×＋」になるということは、つまり、片方がプラスに振れているのに、片方が逆方向のマイナスに振れているということで、「逆向きの関係」と言えます。このように逆向きの関係にある変数ｘ・変数ｙの組合せが多く観察されると（＝マイナスの面積が多い）、分子がマイナスになり、「マイナスの相関がある」と言えます。

相関係数の分母

続いて、残る分母の意味を確認致しましょう。分母に登場するのは、変数ｘと変数ｙそれぞれの標準偏差です。若干紛らわしくて恐縮ですが、分子を計算する際に、変数ｘと変数ｙについて、それぞれの平均から差分を「偏差」と呼び、対になっている変数ｘの偏差と変数ｙの偏差を掛けて四角形の面積を計算しておりました。つまり、分母の計算は、変数ｘの偏差同士・変数ｙの偏差同士を掛け算（二乗）して面積を出しましょう、という話になります。

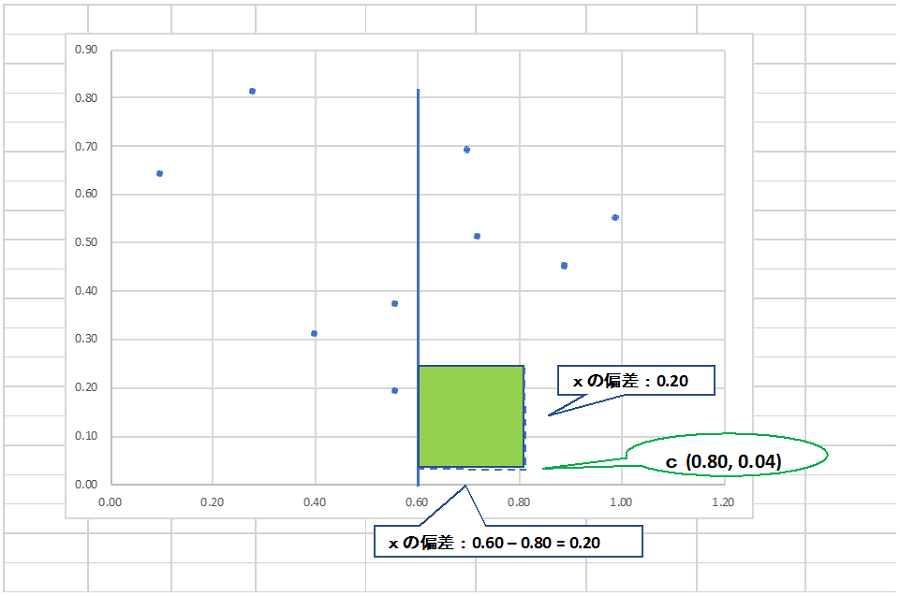相関係数（偏差計算）図2：相関係数（偏差計算）

上記図2では、組合せc点（ｘ：0.8, ｙ：0.4）から、変数ｘの偏差＝0.2（0.8-平均）を使って面積を描いています。二乗するので正方形になります。また、偏差がマイナスであっても（二乗なので）、面積は必ずプラスになります。図2では正方形を一つしか描いていませんが、数値例では、変数ｘと変数ｙの組合せが10組ありますので、変数ｘで10個、変数ｙで10個、合計20個の正方形が描かれることになります。最後に、10個のｘ正方形を足して、平方根を取れば、変数ｘの標準偏差が導かれます。

変数ｙについても同様の計算を行います。平方根を取る作業は、10個の正方形を足し上げると大きな面積の正方形ができあがるので、その一辺の長さを求めます。変数ｙの方でも10個分正方形を足し上げますので、それを平方に開いて、一辺の長さを求めます。プラスの面積の平方根を取るので、変数ｘも変数ｙも正になります。

これでようやく分母が計算できます。変数ｘと変数ｙの標準偏差（それぞれ正方形の一辺のイメージでした）を掛け合わせると、またもや四角形ができあがりますが、それが分母＝標準偏差の積になります。

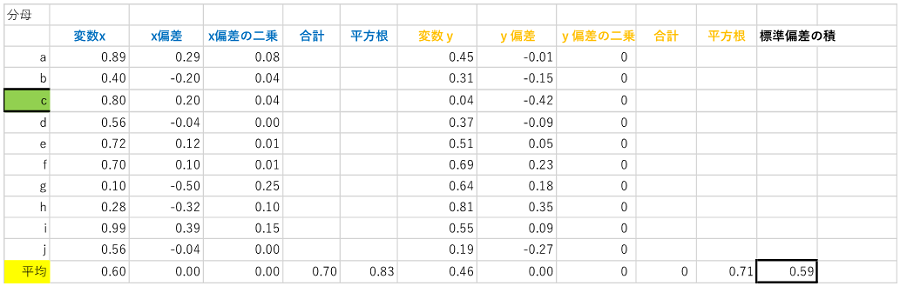相関係数（標準偏差の積）表2：相関係数（標準偏差の積）

相関係数の算出

前置きが長くなってしまいましたが、やっと相関係数を計算できるようになりました。

相関係数  
分子： -0.18
分母： 0.59
分子／分母： -0.31

表3：相関係数（結果）

繰り返しになりますが、分子は、変数ｘと変数ｙについて、それぞれ、平均からの差分によって、四角形の一辺を作り出し、それぞれの四角形の面積を計算して、合計を取る。その時、辺の長さには符号があるので、違う符号を持つ辺の組合せが多い場合は、足し合わせた四角形面積もマイナスになる場合があります。

結局のところ、分子だけ計算すれば、相関について議論できそうな感じもあります。ただ、分子だけですと、プラス・マイナスの傾向しか議論できません。どんな数値例が来た場合でも、相関度合いを比較できるよう「基準化」しておく必要があります。そのために、分母で分子を割っておきます。

そのイメージとして、下記表4をご覧下さい。変数ｙだけ100倍してあります。例えば、元々変数ｘもｙも単位がメートルだった所を、変数ｙだけセンチに置き換えた場合を想起下さい。結果、分子の面積＝ｘとｙ共分散の値が変わっております。当然かもしれませんが、分子だけを見ていると、単位の変化などに値が影響を受けます。

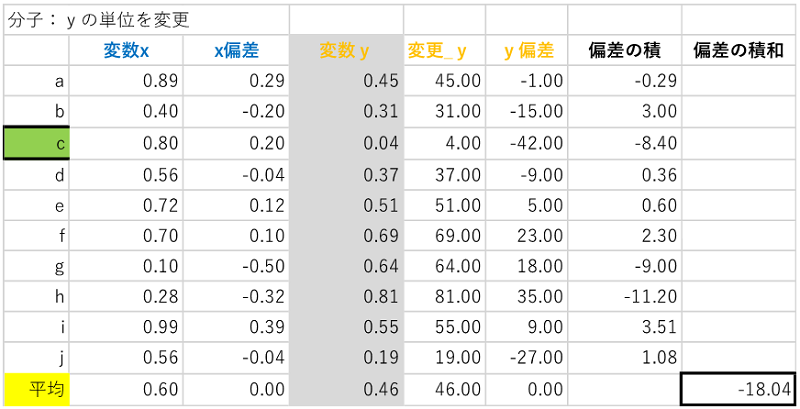相関係数（偏差の積和　単位変更後）表4：相関係数（偏差の積和　単位変更後）

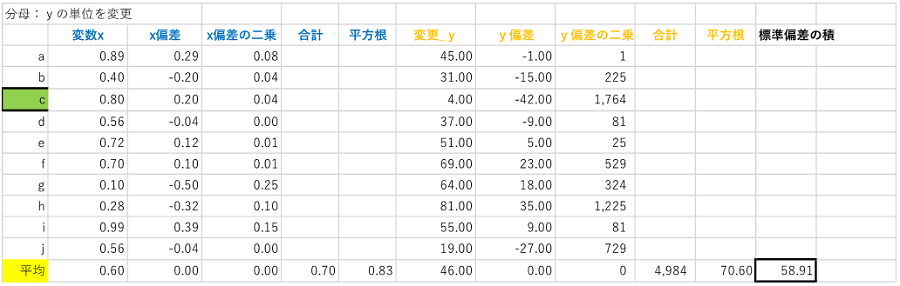相関係数（標準偏差の積　単位変更後）表5：相関係数（標準偏差の積　単位変更後）

当然の結果ですが、分母の結果も変わります。したがって分母を考慮に入れると、分子と分母の変動分が相殺されて、相関係数の計算結果自体は変わらない、ということになります。ぜひお手元でお試し下さい。

ところで、数値例から求めた相関係数の「-0.31」というのは、果たして相関があるのか、無いのか…？一概には言えませんが、「やや（負の）相関がある」という表現になりましょう。見方によっては「無い」と表現される方もあるかもしれません。その辺は議論しても仕方無いですが、数値で表現されるとありがたみがあります。

（以上）

コラムニスト
公共事業本部　ソリューションストラテジスト　松村　俊英

関連コラム

カテゴリー一覧へ戻る