コラム

デジタル社会形成に向けて　第2章（15）～自治体DXの先に～

2023.05.15

訪問型行政サービスの効果測定を下記フローに沿って説明してきております。（下図記載）

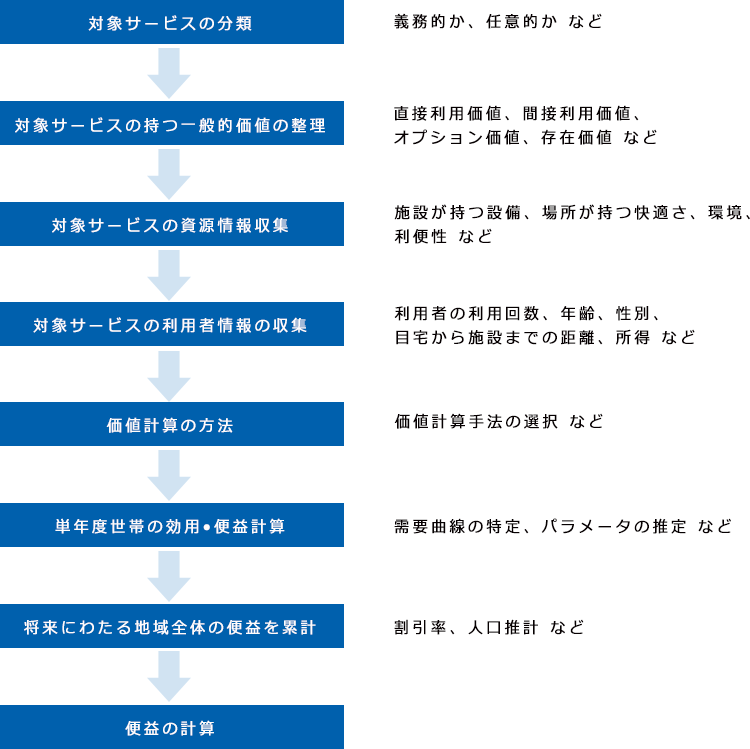図1：訪問型行政サービスにおける効果測定フロー

前回からの続き

潜在クラス分析によってセグメント化されたサンプルについて、どのような属性が選択行動に影響を及ぼすのか？を把握するため、選択行動の推計に入る前の準備作業の一環として、回帰分析のおさらいを進めています。

前回のコラムで、統計分析ソフトウェア「R」の統合開発環境「R studio」に用意されているiris （アイリス；あやめ）のデータセットを使って、回帰分析を行いました。下記（図2）の散布図を参照いただくと、縦軸に「がく_長さ」、横軸に「花弁（かべん）_長さ」が取られています。「がく_長さ」を「花弁_長さ」によって、「直線的な関係」として説明しようとした結果として、右肩上がりの直線で表現されます。

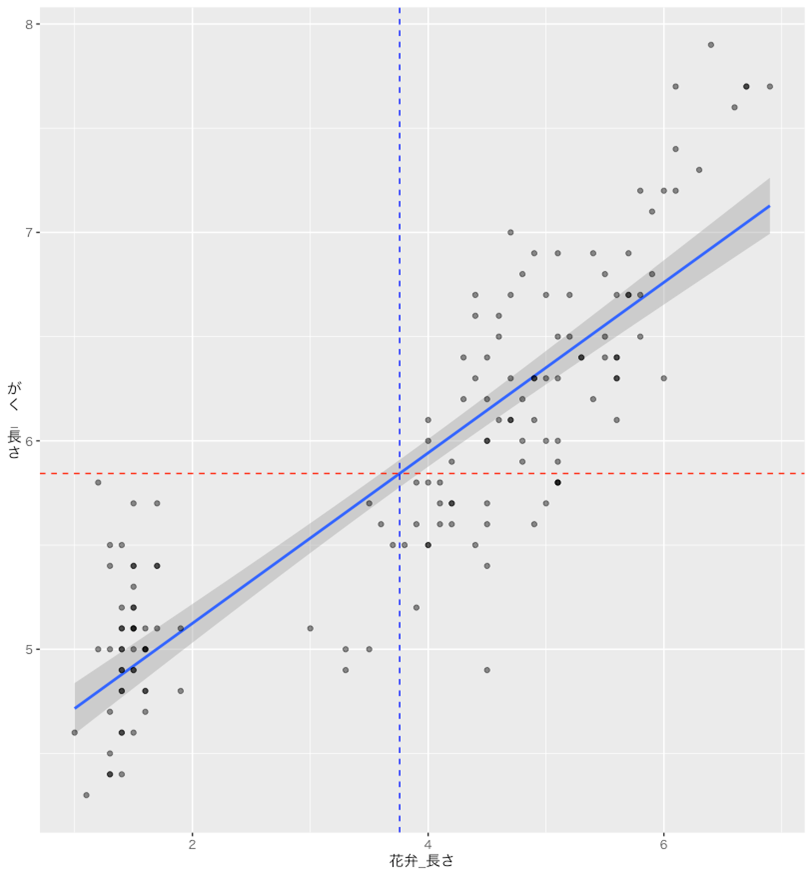図2：散布図

さて、次なる関心事ですが、この推計は、どの程度「決定力」があるのか？という話です。ここで登場するのが「決定係数」でした。では、ここで言う「決定力」とは、何を意味しているのでしょうか。下記の集計結果のとおり、決定係数は0.758となっておりました。

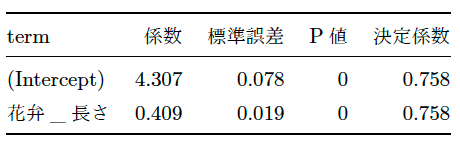表1：集計結果

決定力を確認するために、回帰分析とは何だったかを振り返ります。今回の事例では、irisの「がく_長さ」と「花弁_長さ」の間には関係があり、例えば、「花弁が長い方が、がくも長いのではないか？」という仮説が正しいのかどうかを確認することになります。

まずは「がく」の長さと「花弁」の長さが一対になったデータ群を集めて、さらにその関係を「直線関係」と見立てました。勿論、「曲線」的な関係である可能性もあり得るのですが、まずは、分かり易く直線関係＝線型を仮定します。

その時、2つのデータ群の間には、無数の直線が引けるのですが、その中の一本を選定するために、「最小二乗法」という選定基準を導入致しました。これは、残差、すなわち、無数にある候補の中から、適当に選択した直線（予測値を繋げたもの）の内、最も、実際の数値群（この場合は「がく」の長さデータ）との差の二乗和が最小になるような一本の直線を選択しました。

したがって、「決定力」の定義を明確にすると言われたら、この残差、すなわち、実際の数値と予測値の差が「小さい」と言えれば良いかもしれません。

決定係数とは

とは申せ、何と比べて「小さい」と言えば良いか？多少、思案を要するところですが、再度、上記（図2）の散布図をご覧下さい。

色・破線の水平線が、大体5.8くらいの所から横に伸びております。この5.8というのは「がく」の長さの単純平均になっております。実際にプロットされている各点については、それほど平均周りに集まっている訳でもなく、平均より大きかったり小さかったり、それなりに散らばっております。話を単純にするために、平均より大きい方について考えてみると、この「平均より大きい」という理由を、今回、「花弁が大きいから」という点に求めようとした訳です。

本当にそのような「因果関係」があるのかどうかは分かりません。逆（因果関係がない）の可能性もあります。いずれにせよ、上記（図1）の散布図の傾向として、「がく_長さ」と「花弁_長さ」には右肩上がりの関係が観測できた訳です。それならば「がく」の長さの平均を上回る部分は、「花弁」の長さが「押し上げている」と解釈しても、決して間違ってはいないでしょう。

では、その「押し上げ効果」は？という事なのですが、それこそが、この直線の傾きになります。今回の推計では0.4ということになってますので、花弁の長さの40％ほどを、「がく」の長さに上乗せすれば、だいたい「がく」の長さになるのでは？という関係を導き出したのです。この時、ｙの平均値から上乗せされた部分は、正に、ｘによって確実に説明できる割合、決定されたと言って良い割合、という解釈ができるのではないでしょうか？

さて、急に鹿爪らしい（※1）書き振りになって恐縮ですが、ここで、実際のデータとデータ全体の平均値との差を「全変動」、推定された回帰式から得られた予測値とデータ全体の平均値の差を「回帰変動」、実際のデータと推定された回帰式から得られた予測値との差を「残差変動」と呼称します。回帰変動が上記散布図中の緑色枠の部分、残差変動が赤色枠の部分、緑色と赤色枠の合計が全変動になります。

決定係数というのは、回帰変動（の平方和）を全変動（の平方和）で割ったものになります。平方和にするのは、分散の計算でもお馴染みですが、各点の平均からの乖離については、プラスもマイナスもあるため、絶対値的な数値の方がありがたいです。とは申せ、絶対値は計算が複雑になるため、二乗でお願いします。

ということで、irisの例では、「花弁」の長さによって、「がく」の長さを約76％説明できる、という解釈となりました。他方で、約24％は決定できない（説明できない）と言えます。解釈として、一つの変数（説明変数）によって、他の変数（被説明変数）の動きを7割以上説明できるのは凄い！ということかも知れません。他方で、100％近くまで説明できるようにしたい！となりますと、「花弁」の_長さ以外の変数を見つけてくる必要が生じます。

いずれにしても、「がく」の長さと「花弁」の長さについては、密接な関係があることは間違いありませんが、これだけでは因果関係までは解りません。そこを解き明かすには、植物に関する専門的な知見が必要になるでしょう。また、統計処理にも工夫が必要になるでしょう。

（以上）

コラムニスト
公共事業本部　ソリューションストラテジスト　松村　俊英

参考

※1もっともらしいの意味（鹿爪は当て字）

デジタル社会形成に向けて 第2章（15）～自治体DXの先に～

前回からの続き

決定係数とは

参考

関連コラム

デジタル社会形成に向けて　第2章（15）～自治体DXの先に～