コラム

  1. HOME
  2. コラム
  3. データ分析
  4. デジタル社会形成に向けて　第2章（9）～自治体DXの先に～

デジタル社会形成に向けて　第2章（9）～自治体DXの先に～

2022.10.03

訪問型行政サービス（A公園の訪問価値）の効果測定を下記フローに沿って説明してきております。（下図記載）

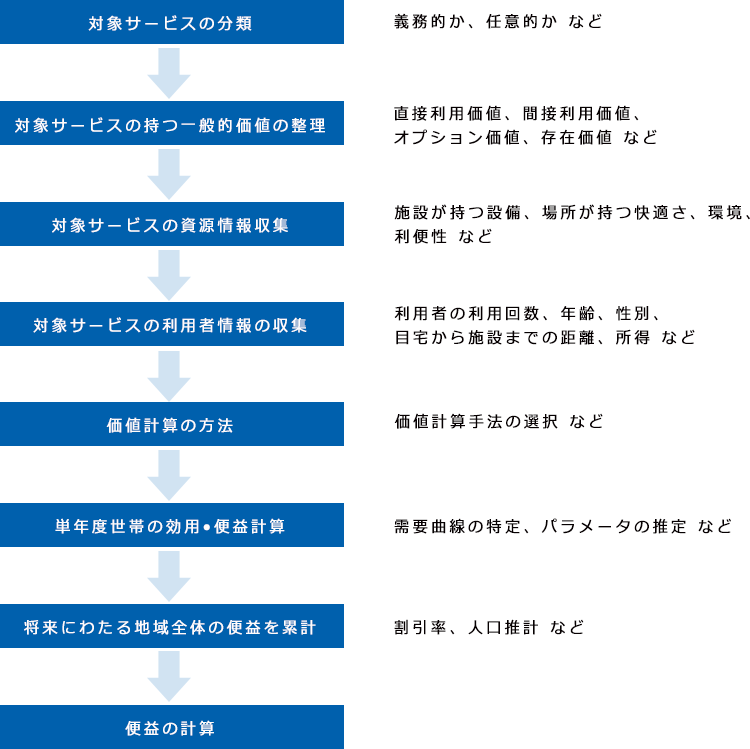訪問型行政サービスにおける効果測定フロー図1：訪問型行政サービスにおける効果測定フロー

前回からの続き～潜在クラス分析とは

前回に引き続き、分析の対象とする大きなグループを「属性に応じてより小さなグループに良い感じに分類してくれる手法」について検討しております。「潜在クラス分析」と呼ばれる統計的手法です。この手法が優れている点は、似たような特徴や行動をする個人をまとめて、そこからグループ分けして、そのグループの特徴を浮かび上がらせてくれることです。
　
潜在クラス分析（latent class analysis, LCA）とは、「分析の対象となる母集団は複数の観測されない部分母集団から構成されている」と仮定する分析手法です。この手法では、観測された個体を異なるカテゴリ（クラス）に分類することが可能になります。その際、個体は1 つのクラスに最初から分類されてしまうのではなく、各クラスへの所属確率が示されます。その結果、仮に3つにクラスが分類されたとして、事後的に、個体を特定のクラスに帰属させることが可能になります。個体ごとに示された各クラスへの所属確率の中で、最も高い所属確率を示したクラスに個体を帰属させるということになります。

潜在クラス分析の活用例について

潜在クラスを使った分析は、すでに多くの事例が存在しております。例えば、柘植隆宏・栗山浩一・三谷羊平著『環境評価の最新テクニック』（※1）という書籍において、環境政策評価の分野で有望視される手法として、潜在クラスモデルの紹介が行われております。

簡単に紹介しますと、「海岸の水質改善の効果」について、数種類の水質改善の代替案を回答者に示し、もっとも 好ましいものを選択してもらうことで、水質改善の支払意志額を推定する、という「選択型実験」の例が挙げられております。この時、通常は、回答者が同一の選好（考え方）を持っていると 仮定される場合が多いでしょう。しかしながら、海岸利用には、海水浴、釣り、サーフィン、ボート、散歩などさまざまな利用形態があり、利用形態が 異なると利用者の水質に対する価値が異なると考えられます。

例として、海水浴 やダイビングなどのように海水の中に「入る」利用者は、散歩のように「入らない」利用者よりも水質に対して高い価値を持っていると考えられます。また回答者の中に海岸を全く利用しない人も含まれる場合は、非利用者は水質に対して低い価値しか持っていない可能性も考えられます。このような場合に、回答者を複数 のクラスに分けて、各クラス別に推定を行う潜在クラスモデルが有効になるという訳です。

このような特徴を持つ分析手法であるため、マーケティングの分野でも早くから活用されております。例えば、ID 付きPOS データに対して潜在クラスモデルを適用し、顧客の購買行動パターンをもとにした新たな顧客セグメントの創出方法を提案したりするなどです。

　それ以外では、サービス選択の分析において援用されている例もあります。例えば、観光・レジャーを旅行目的とした訪日外国人旅行者の、目的地への選択パターンの特性把握に、潜在クラス分析を活用する事例などがあり、例を挙げ出すと、枚挙に暇がございません。（※2）
蛇足ながら潜在クラス分析を行う際には、統計ソフトなどを利用することになりますが、有償のものは元より、Rなどの無償ツールにおいても幾つかの分析パッケージが提供されております。

クラス（グループ）分けについて

前回のコラムにおいて、訪問型行政サービス利用に際して、600人程度の市民を対象に調査を行った結果から得られたサンプルデータが示す「大まかな属性」を提示致しました。これらのサンプルを改めて無作為に並べ替えをして、クラス（グループ）分けしてしまおうということです。

ここで問題になるのが「幾つのクラスに分けるか？」という点です。分析者の好みで、3つとか5つとか、決めてしまって良ければ、そうしたい所ではあるのですが、「クラスを幾つに分けるか？」については、一応の指針と言いますか、基準がございます。詳細については、難しい話となるため割愛させていただきますが、統計ソフトの操作自体は簡単です。

統計ソフトにおいては、クラス数ごとに「BIC 値」（※3）あるいは「AIC 値」（※4）と言われる数値を計算し、その数値が最も小さいクラス数を採用する、という手順を用います。例えば、クラス数を1～5 くらいまで順番に測定して行き、仮にクラス数5の時に、一番小さい数値が計算されたとしたら、「クラス数は5である＝5つにグループ分けする」ということになります。
　
実際に統計ソフトを使って計算してみると、BIC 値とAIC 値が推奨するクラス数が一致しない場合もあります。そんな時は、BIC値 の方がサンプルサイズに影響を受けずクラス選択を行える性質を持っている、とされているため、BIC値 の数値によってクラス数を判定することになります。
　
今回の例ではBIC値を計算した結果、「クラス数は3」となったと致しましょう。因みに、「クラス数1」は、クラス分けをしない場合を意味しております。BIC値を計算してみて、クラス数1の場合に最小値を取ったなら、「クラス分けしなくても良い」ということになります。

（以上）

コラムニスト
公共事業本部　ソリューションストラテジスト　松村　俊英

参考

関連コラム

カテゴリー一覧へ戻る