コラム
デジタル社会形成に向けて（7）～自治体DXの先に～
2021.12.06
需要と供給を並べてみると
前回までのコラムにおいて、「窓口業務のDX化」を例として、発生する需要側の便益と、供給側の業務改善効果を計測してきました。
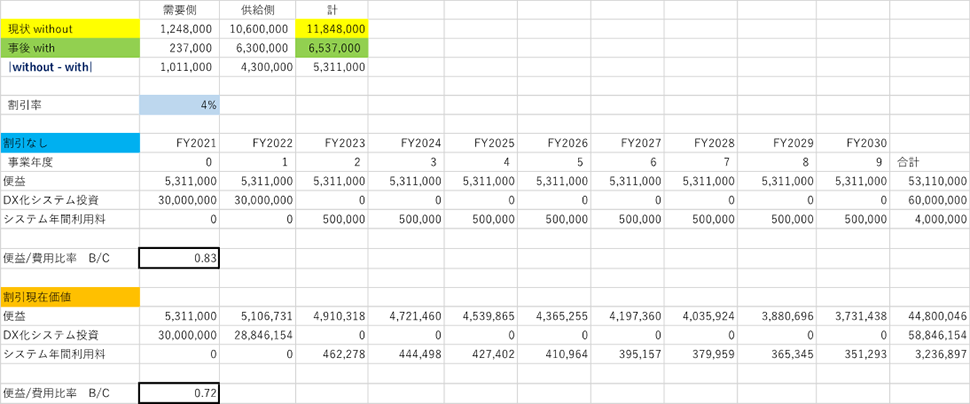表 サービス業務コストのbefore/after（総効果）
まず「単年度」の総効果ですが、上記の表の一番上をご参照ください。before＝DX化しない場合については、黄色の網掛け。after=DX化実現の場合については、緑色網掛けにそれぞれ計算結果が表示されております。列には「需要側」・「供給側」、行には「現状before(without)」・「事後after(with)を取っております。
上記の結果から、需要側の変化を見ると、1,248千円マイナス237千円＝1,011千円のコスト削減効果が生じております。これは、行政のDX化によって、住民が自由に使える時間が増えたという意味で、ある種の所得創出効果とも言えましょう。自由に使える時間で賃金が伴う仕事を行なえば、時間を貨幣化する事ができます。
供給側の変化を見ると、10, 600千円マイナス6,300千円＝4,300千円のコスト削減効果が生じております。すなわち、ある1つの窓口業務をDX化することで生じる地域（住民と役所）に生じる貨幣的な効果は、合計で5,311千円になりました。
結局、DX化の効果は？
これまでの議論には、大きく2つの要素が欠けております。1つは申すまでもなく、DX化に掛かった投資費用を考慮に入れていない点。もう1つはDX化投資の効果は、単年度だけではなく長く続くため、複数年の視点を考慮に入れていない点。もちろん、それ以外の要素もあるでしょうが、今回は捨象しておりますのでご了承ください。
以上の2点を議論に組み込むと、上記の表の中段に記載されたものになります。行には「DX化によって創出された便益」・「システム投資額」・「システム年間利用料」が表記されております。（※1）列には「事業年度」が表記されております。
今回の場合、以下の条件で算出しております。繰り返し申し上げますが、条件については変更可能ですので、一例としてご覧ください。
結果、目を右に移していただきますと、10年間で、得られる便益の総計は53,110千円。発生するDX投資プラス利用料の総計は64,000千円となり、結果的にシステム投資額が便益の発生額を上回っております。その比率は、「便益／費用比率」＝0.83と示されております。
それではDX化は失敗ではないか？と思われたでしょう。確かに、1つの窓口業務をデジタル化しただけでは元が取れなかった、という例になっております。しかし、2つめの窓口業務を同じプラットフォームに乗せて、スマートフォンに移し替えたらどうなるでしょうか。更に3つめをスマホ化したら…。この時に問題となるのは、追加的システム投資の発生具合でしょう。窓口業務のスマホ化を進めれば進めるほど住民の便益も増えますが、それと同じ比率でシステム投資が増えたのでは意味がありません。
そのため、DX化を進める際のプラットフォームとして、追加的費用が便益の増加率を下回る様に設計すべきです。幸いにも、昨今のシステムはクラウドモデルが普及しており、追加的費用がかなり低く抑えられる様になっております。今回の簡単なモデルでは、システム的追加投資は発生しない前提になっておりますので、2021年度か2022年度に、あと1つでも最初の事例と同様な窓口業務をスマートフォンに移せば、投資額を上回る便益を回収できる、ということで大団円を迎えます。
あとがき
今回のコラムは終了となりますが、最後に「割引なし」と「割引現在価値」について、付言致します。ここは、「今年の100万円と10年後の100万円の、現時点での価値を同じと考えて良いか？」という、些か（いささか）哲学めいたお話です。詳細な議論は本稿の範囲を超えますので、興味のある方向けに概要だけご紹介いたします。
例えば、今回の便益計算において、需要側には年間100万円分の時間節約効果が発生していました。仮に、時間節約の恩恵を被った住民の皆さんが、その浮いた時間で仕事に精を出したとします。そうすれば、単なる計算上の「効果」がリアルな「収入」として現前する訳です。この仕事で得られた報酬（収入）を銀行に預金するとしましょう。仮に年利4％とします。その際、1年後に100万円となって戻ってくる、今年の預金額は幾らになるでしょうか？
答えは年利4％ですから、約96万円（100万円／(1+0.04％)^1）になります。また、2年後に100万円となって戻ってくる、今年の預金額は約92万円（100万円／(1+0.04)^2％）となります。計算式内に「＾2」とあるのは、「2乗」の意味です。今年96万円を預金すれば、1年後に100万円となり、今年92万円を預金すれば、2年後に100万円になる。この時、1年後の100万円は現在の96万円と等価であり、2年後の100万円は現在の92万円と等価である、と考えることができないでしょうか？
この考え方（＝割引現在価値）が首肯（※2）されるなら、現在に近い貨幣価値は大きく、遠い将来の貨幣価値は小さく評価される事になります。難解ではありますが、効果が長期に及ぶ投資効果について、時間軸上の重み付けを考慮する場合に、割引現在価値の考え方が使われます。今回の便益計算の事例で言うと、できるだけ早くDX化を進めて便益を大きくした方が、時間軸上でみた場合にも、結果的に便益が大きく計算される、という結論に至ります。
コラムニスト
公共事業本部 ソリューションストラテジスト 松村 俊英
参考
- ※1「割引なし」の項目については、あとがきに記載されている「割引現在価値」に関わる項目になります。
- ※2うなずくこと。承知すること。