コラム

  1. HOME
  2. コラム
  3. データ分析
  4. 木も見て森も見たい（９）～公共資本ストックと地価に関係はあるか～

木も見て森も見たい（９）～公共資本ストックと地価に関係はあるか～

2021.01.13

前回からの続き

地方公共団体が保有している「資本ストック」＝固定資産の簿価が、地域の地価を押し上げる効果が有るのかどうかを推計してみよう、というお話でした。幸いにもバランスシートから複数年にわたる簿価データを取得（※1）できるため、そのデータを使います。

今回扱うデータは、個別自治体ごとに時系列にデータを持っているため、「パネルデータ」と呼ばれます。パネルデータの利点は色々有ると思いますが、例えば、北村(2005)(※2)によれば、「パネルデータは膨大なクロスセクションデータ(※3)を複数年にわたって結びつけたものであり、その情報量は極めて大きい。これによって、多重共線性の問題は解消され、推計上の自由度は増し、推計の不偏性は向上する。」ということだそうです。

多重共線性とは、重回帰分析などを行う際に説明変数間に強い相関が有ると、パラメータの推計に偏りが出てしまうことです。

パネルデータの種類

折角なので、ここでパネルデータの種類を整理しておきましょう。同じく北村(2005)（※2）を参考にします。

  • プーリング・データ(Pooling)：
    時系列、クロスセクションのデータを全て合体して全ての変数が共通の母集団から発生していると考える。通常の最小二乗法と同じ結果になる。
  • ビトウィーン・データ(Between)：
    時系列方向に個別主体毎の平均を取り、それをクロスセクション・データとして分析する。このデータでは時系列方向の変動ではなく、個別主体間の違いを見ることに主眼をおいたもの。
  • ウィズイン・データ(Within)(固定効果モデル)：
    個別主体毎の時系列方向のデータのみを扱うものである。個体ごとに個体内偏差（時点ごとの観察値から個体内平均を引き算した値）を求め，それらによって回帰分析をする。
  • 切片は個体(地方公共団体)ごとに異なるが、パラメータは共通となる。
  • 導入し損なった変数(欠落変数バイアス)が時間とともに変化しないなら、切片の推定値が歪むだけでパラメータは正しく推定できる。

これ以外の論点としては「変量効果モデル」が有ると思いますが、当コラムの範囲を超えてしまうため、割愛させていただきます。

データの中身

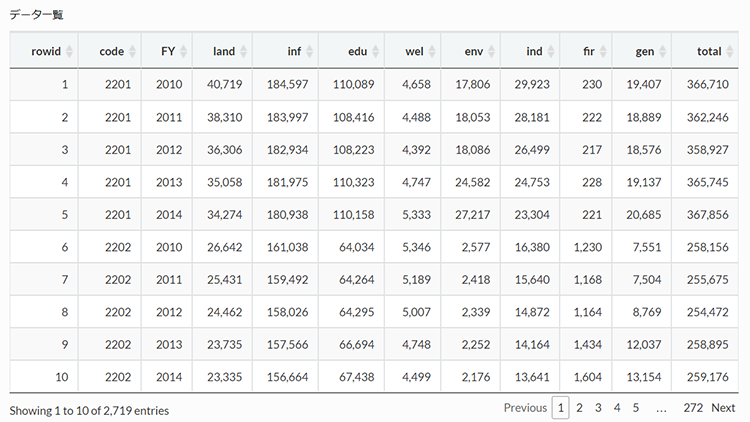
データの確認を致しますと、「land = 住宅地の地価、inf = 生活インフラ・国土保全、edu = 教育、wel = 福祉、env = 環境衛生、ind = 産業振興、fir = 消防、gen = 総務」となります。会計は普通会計ベース。FYは会計年度を示しており、2010年度から2014年度まで。単位は千円です。

データ一覧（タップすると拡大表示されます。）
データ一覧

    # データの読み込み
library(psych)

# ディレクトリの指定
setwd("/Users/tm/Dropbox/_Study/Ebisu/")
# データの読み込み
# View(fs_data)
fs_data <-    
    read_csv("./200907_fs_data.csv") %>%
    # 名称変更、正規化せず
    rename(land = 4, inf = 5, edu = 6, wel = 7, env = 8, ind = 9, fir = 10 ,gen = 11) %>%
    # ゼロデータを削除
    filter(code != 13102) %>%
    # 合計値を挿入
    nest(inf : gen) %>%
    mutate(total = map_dbl(data, ~ sum(.))) %>% unnest(data)

# データ一覧    
  fs_data %>%
    datatable(
        caption = "データ一覧",
        rownames = F) %>%
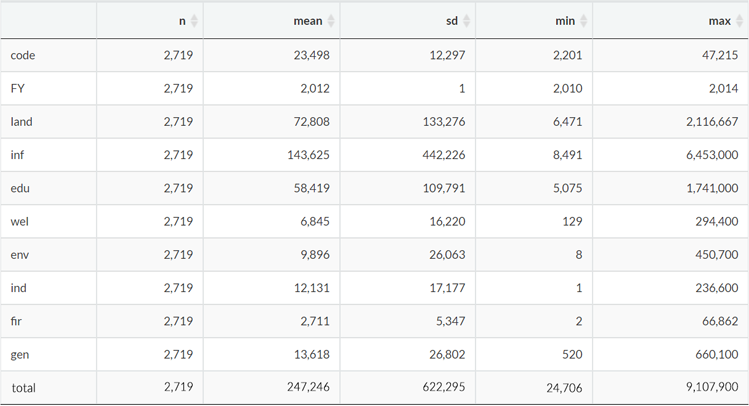
    formatCurrency(columns = c(4 : 12),  currency = "",  mark = ",",  digits = 0)

データの基本的な統計量も合わせて示します。「n = サンプルサイズ、mean = 平均、sd = 標準偏差、min = 最小値、max = 最大値」になります。なお、直感的に各説明変数間に相関が有りそうですが、ここでは無視して先に進みます。

基本統計量（タップすると拡大表示されます。）
基本統計量

library(corrr)

# 基本統計量
  fs_data %>%
    describe() %>% slice(-1) %>% select(-c(1, 5, 6, 7, 10 : 13)) %>%
    datatable(
        caption = "基本統計量") %>%
    formatCurrency(columns = c(1 : 5),  currency = "",  mark = ",",  digits = 0)

いよいよ推計

では、実際に推計してみましょう。統計ソフトには必ずといってよいほど、パネルデータを使ったパラメータ推計ができるパッケージがあると思います。今回用いるRの場合は、plmパッケージ内にあるplm()関数を使うと便利です。書式は、通常Rで回帰分析を行う際に利用するlm()関数と基本的に同じですが、データのフォーマットをパネルデータ用に整形する必要があります。整形するツールはplmパッケージ内に同梱されていますので、作業上は悩むことは無いと思います。

まずは、PooledOLSということで、時系列も地方公共団体別の情報も持っているパネルデータではありますが、その辺の個別効果は無視して一気に回帰分析してしまおうというものです。OLS（Ordinary Least Squares regression）とは、最小二乗法のことです。それから、推計に際しては、被説明変数、説明変数ともに対数をとります。

Pooling Model

Call:
plm(formula = log(land) ~ log(inf) + log(edu) + log(wel) + log(env) + 
    log(ind) + log(fir) + log(gen), data = fs_plm, model = "pooling")

Unbalanced Panel: n = 544, T = 4-5, N = 2719

Residuals:
     Min.   1st Qu.    Median   3rd Qu.      Max. 
-2.239332 -0.338381 -0.013066  0.305835  2.480033 

Coefficients:
              Estimate Std. Error  t-value  Pr(>|t|)    
(Intercept)  7.0907060  0.1457194  48.6600 < 2.2e-16 ***
log(inf)     0.1285619  0.0276737   4.6456 3.552e-06 ***
log(edu)     0.3283104  0.0352552   9.3124 < 2.2e-16 ***
log(wel)     0.2870671  0.0181679  15.8007 < 2.2e-16 ***
log(env)     0.0164600  0.0099079   1.6613   0.09677 .  
log(ind)    -0.3911991  0.0075682 -51.6901 < 2.2e-16 ***
log(fir)    -0.0153112  0.0126298  -1.2123   0.22550    
log(gen)    -0.0330046  0.0204295  -1.6155   0.10631    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Total Sum of Squares:    2414.4
Residual Sum of Squares: 770.24
R-Squared:      0.68098
Adj. R-Squared: 0.68016
F-statistic: 826.701 on 7 and 2711 DF, p-value: < 2.22e-16


library(plm)

# plmで扱えるデータセットに変換
fs_plm <-
    pdata.frame(fs_data, index = c("code","FY"), drop.index = T)  
# 分析を実行
# pooledOLS  
pooling <-
    plm(log(land) ~ log(inf) + log(edu) + log(wel) + log(env) + log(ind) + log(fir) + log(gen), data = fs_plm, model = "pooling")
    summary(pooling, robust = T)

Rから出力されたそのままをお示ししておりますので、見慣れない方にはかなり気持ち悪い感じになっているかと思います。

Call: とある部分は、今回実行した推計式です。幾つか飛ばして、Coefficients： のところにある Estimate の列が係数の推定値です。(Intercept)とあるのは、切片です。その横にある Std.Errorというのは推定量の標準誤差。t-valueとあるのはt値です。Pr(>|t|)はP値です。その横についている***という印は、その説明変数が有意であったかどうかを示すものです。R-Squared: とあるのは、決定係数。Adj. R-Squared: は自由度修正済み決定係数。F-statistic: とあるのはF値のことですが、ここでのF値は今回の推定結果、すなわち、係数の値が全てゼロであるという帰無仮説を検定するものであり、p-value はそのP値になります。

と申し上げても何のことやら…、という方もいらっしゃると思いますので、次回、少々用語の説明をさせていただきます。

コラムニスト
公共事業本部　ソリューションストラテジスト　松村　俊英

参考

関連コラム

カテゴリー一覧へ戻る