コラム

デジタル社会形成に向けて　第2章（18）～自治体DXの先に～

2023.08.07

訪問型行政サービスの効果測定を下記フローに沿って説明してきております。（下図記載）

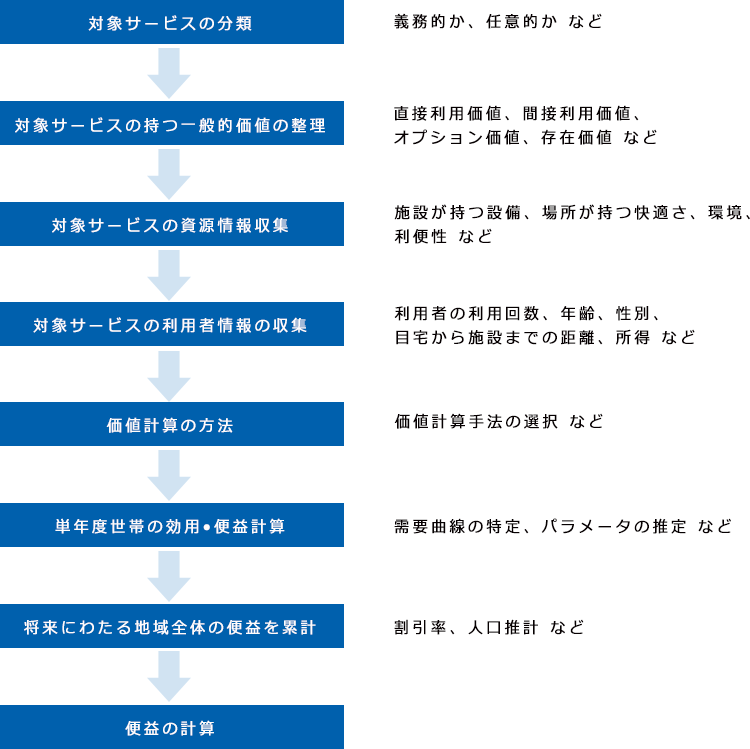図1：訪問型行政サービスにおける効果測定フロー

前回からの続き

前回までのコラムで、「yes／no」「0／1」「買う／買わない」「行く／行かない」といった選択問題を、ある種の確率分布に紐付けて考えてみましょう、というお話をした上で、正規分布を「仮定する／しない」といった、それぞれのパターンを概観してみました。

実際に計算してみる

今回は、ある要因(変数)が選択結果に対してどのようなインパクトを持つモノか、簡単な数値例(サンプル)を使って、実際に推計してみます。具体的な形としては、下記のようなパターンの式を推計して、係数の数値がどれくらいになるかを推計したいということになります。

公式1｛yes / no｝ ← 定数 + 係数 * 説明変数

単純な直線の回帰では駄目だということは、前回・前々回のコラムで説明済であるため、Ｓ字を上下に引き延ばしたような曲線で推計してみることになります。今回使用するデータは、ｙを「中央図書館利用の有無」、ｘを「1週間の読書時間」とした、ごくシンプルなものです。ｙが選択結果で、ｘがその要因を決める元になった(と思われる)要因です。途中から省略していますが、実際のデータサイズは20あるとお考え下さい。

図2：データ集計結果表1：データ集計結果

ｙについては、1が「利用する」、0が「利用しない」を示しています。1週間の読書時間と、図書館利用の有無の関係はどうなっているか？と把握するのが目的です。では、実際に公式1の定数と係数を求めてみます。
その前に、前々回のコラム内容を思い出していただきたいのですが、0／1のどちらかしかなく、また、右端と左端に偏った分布をしている場合、それらを直線で近似するのは意味不明になるため、S字が間延びしたような曲線で近似したのですが、その際の近似の仕方をロジスティック回帰と呼んでおりました。そして、この「S字への引き延ばし方」は、少々面倒な手続きを踏む必要があります。

1. 0と1からなる2値データｙが、ｙ＝1となる確率をPとする。
2. その時、ｙ＝ 0となる確率は1 − P となる。
3. 次に、Pと1 – Pの比を取る(「オッズ比」と呼ばれています)。
4. 「オッズ比」の対数を取る。
5. Pについて整理する(逆数関数を作る)。

上記の手順を踏むと、前々回のコラムで紹介した、下記のロジスティック関数が登場します。

数式１　P = 1 / (1 + exp(-1 * z)) (再掲；記号は変えています)

ロジスティック関数を図示すると、前回のコラムで紹介した下記図2の通りです。横軸のｘがどんな値を取っても、縦軸のP(と読み替えます)は、0から1の間に収まる様になっております。しかも、ｘの値は0近傍と1近傍に固まって分布しており、0／1しかない世界を、近似するのには都合が良い訳です。

そして、上記数式１のzが、「z = 定数 + 係数 * 説明変数ｘ」となっている事を受けて、いよいよ、この定数と説明変数ｘの係数を推計することになります。

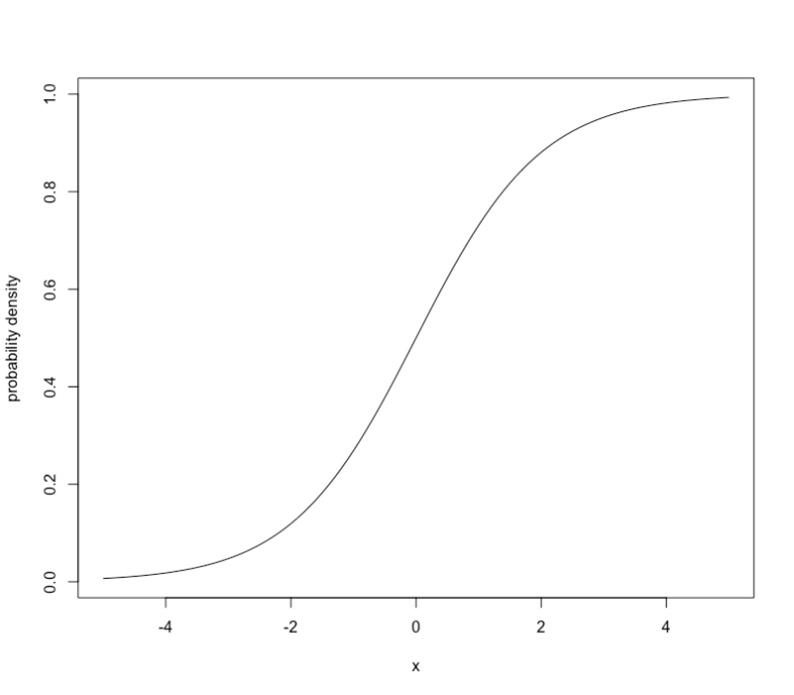図2：(再掲) 標準正規分布の累積分布関数

どうやって推計するか

いきなり出鼻を挫かれるのですが、ご覧の通り、上記図2はS字が間延びしたような曲線形状のため、直線で近似する場合に利用した「最小二乗法」を用いる事ができません。何か別の方法で推計することになりますが、最小二乗法以外に、どのような方法で推計値を算出すれば良いか？

ここで登場するのが「最尤法（さいゆうほう）」という推定値の算出方法です。「尤」という漢字は日常生活でお目に掛かる機会はありませんが、「もっともらしい」と入力変換すれば、「尤もらしい」と表示されます。すなわち、「何だか良く解らないけども、適当な数値を入れて(定数とｘの係数)、ある事柄(今回は、図書館を利用する／しない)が起こる確率を、手当たり次第に計算してみて、結果、一番確率が高くなったときに、その値を推定値にする」という、何だか乱暴というか、ダイナミックというか、力業に近い方法です。表1のデータ集計結果から算出すると、下記表2の結果が導かれます。

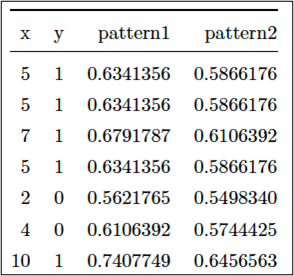表2：集計結果

パターン1は、定数＝0.05、係数＝0.1。パターン2は、定数＝0.1、係数＝0.05として、上記計算式に数値を入れて、「発生確率」を計算してみたものです。これら、発生確率を全部掛け合わせたものが「尤度」ということになります。事例では、2つのパターンしか提示していませんが、もちろん、これら以外にも、無数のパターンがありえるでしょう。そして、それらのパターンの中から最も数値が大きくなった組合せで使った数値(今回は定数と変数ｘの係数)の組合せを、「一番尤もらしい」推計値として採用しましょう、という話になります。

最尤法は、少々乱暴な算出方法な気もしますが、「今回のサンプルでやってみて、尤も発生確率が高くなるから問題ない」とも言えます。ただ、今回は変数が一つでしたが、実務上、最尤法で複数のパラメタ(変数が複数ある場合)を推定する際には、手早く推計を行う必要が生じます。そんな時には、やはり、これまで何度かご紹介してきた「R」のような統計ソフトが威力を発揮致します。次回は、Rを使ってパラメタの推計を行います。

(以上)

コラムニスト
公共事業本部　ソリューションストラテジスト　松村　俊英

デジタル社会形成に向けて 第2章（18）～自治体DXの先に～

前回からの続き

実際に計算してみる

どうやって推計するか

関連コラム

デジタル社会形成に向けて　第2章（18）～自治体DXの先に～