コラム

  1. HOME
  2. コラム
  3. データ分析
  4. デジタル社会形成に向けて　第2章（13）～自治体DXの先に～

デジタル社会形成に向けて　第2章（13）～自治体DXの先に～

2023.03.06

訪問型行政サービスの効果測定を下記フローに沿って説明してきております。（下図記載）

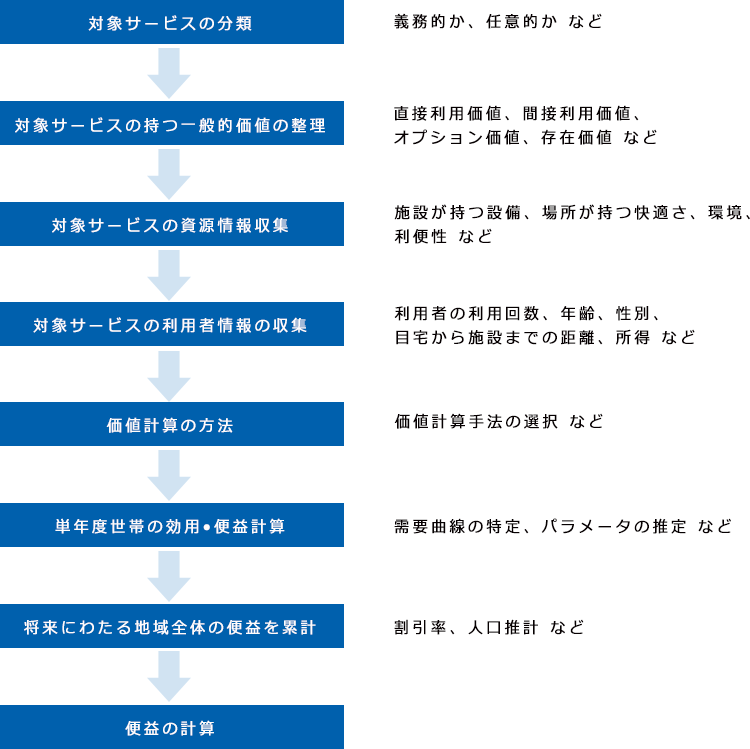訪問型行政サービスにおける効果測定フロー図1：訪問型行政サービスにおける効果測定フロー

物差しを合わせる

前回までのコラムで、相関の意味についてお話をしてきましたが、そもそもの問題意識は、「潜在クラス分析によってセグメント化されたサンプルについて、どのような属性が選択行動に影響を及ぼすのか？」について知りたいということでした。すぐにでも分析に入りたいところですが、正確な分析を行うために必要となる手順に従い、準備を進めているところです。

その準備の一つとして、「標準化」というのがあります。これは何かと言いますと、異なるスケール・単位のデータ同士を上手く一緒に取り扱うために必要となる作業になります。

例えば、ある学生が数学と国語のテスト（各100点満点）を受けて、それぞれ70点取れたとして、「どちらの科目が良くできたのか？」を知りたいと致しましょう。その場合、70点も取れたのでどちらも良くできた、という判断もあろうかと思いますが、このような時、「テストの平均点はどうだったのか？」が気になるはずです。仮に数学のテストが平均90点、国語のテストが平均55点だったとすると、数学のテストは出来が良くなかった。他方で、国語のテストは出来が良かった、という話になります。

下表で示しますと、数学・国語で70点を取ったのは番号4の学生になります。（説明用のため、サンプルサイズは10としています。）標準偏差が出て来ておりますが、これは以前のコラムで説明していますが、平均からの乖離を示す物差しです。分散を平方に開いたものでした。分散は、各データの、平均からの差分を二乗し、全て足し上げて、サンプルサイズで割ったものでした。今回の例ですと、サンプルサイズ10になります。

番号 数学 国語 理科
1 100 60 120
2 95 60 180
3 95 60 50
4 70 70 140
5 90 100 180
6 80 0 50
7 85 100 90
8 85 0 90
9 100 100 100
10 100 0 100
合計 900 550 1,100
平均 90 55 110
標準偏差 9.5 39.3 43.6
分散 90 1,545 1,900
標準化変量 ▲2.11 0.38 0.69
偏差値 29 54 57

表1：採点表（数学・国語・理科）

平均を見るだけでも、「良くできたかどうか？」が分かる感じがするのですが、数学・国語に加えて、理科も比較してみたいのです。ただ、困った事に理科は200点満点で平均点は110点になっております。満点が100点の2倍ならば、得点を1／2にすれば良いのでは？とも思います。それで良い感じもするのですが、もう少し、キチンと説明できる方法がないものでしょうか？

標準化

ここで登場するのが標準化の考え方です。満点が異なるグループ（数学・国語と理科）の平均値を比較するのではなく、それぞれのグループ内における「自分の（得点の）ポジションを出してやれば比較もし易かろう」、という話です。今回の場合、各グループのサンプルサイズ（受験者が10人という想定）ですので、各グループで得点の大きい順／小さい順で順番を数える、というのも良いかも知れません。上から3番目とか下から2番目とか。ただ、国語などは100点が3人も居るので、数えるにしても4番目でもあり、「2番目」でもあったりします。結局、そのグループ内でのデータの散らばり具合も考慮に入れないと比較は難しいです。

データの「散らばり」具合を考慮する際には、分散／標準偏差が役に立ちます。正に、これらの統計量は、散らばり具合を測るために考案されたものですから。上記表にある3科目の標準偏差はバラバラです。従って、番号4の学生のポジションを確認するには、得点（今回の事例では数学・国語が70点、理科が140点）から、それぞれの平均値を引いておいて、それらを各グループの標準偏差で割ってやれば、スケールやばらつきの違うグループでの、「自分の立ち位置」が比較できるようになります。このように整理された変量のことを「標準化変量」と言います。上表に標準化変量の計算結果（番号4の得点について）を示してありますが、これで比較できるようになりました。

偏差値とは？

とは申せ、何となく分かり難いですよね。そこで、更に標準化変量を分かり易い「物差し」に改良したいのですが、そこで登場するのが偏差値になります。受験の時にお世話になるお馴染みの「物差し」ですが、標準化変量を加工して作成されます。すなわち、標準化変量に10を掛けて50を足すだけです。

少しややこしいのですが、標準化を行う際に、平均を引いて、標準偏差で割っていました。要するに、「平均値 ＝ 0、標準偏差 ＝ 1」に変換した訳です。更に偏差値を算出するためには、50を足して10を掛けます。結果として、平均を50、標準偏差を10に変換している事がわかります。50を中心にして、前後に数値がバラつくので、肌感覚で分かり易くなったはずです。

計算式上、番号4の学生が、数学・国語で50点を取っていたなら、偏差値は50になります。また、数学や国語グループの中で、仮に、番号4の学生だけが70点で、残りの9人が50点だった場合、番号4の学生の偏差値は80になります。そのため、標準化変量や偏差値といった「物差し」は、そのグループのバラツキ度合いに依存しますので注意が必要です。

（以上）

コラムニスト
公共事業本部　ソリューションストラテジスト　松村　俊英

関連コラム

カテゴリー一覧へ戻る