コラム
デジタル社会形成に向けて 第2章(14)~自治体DXの先に~
2023.04.03
訪問型行政サービスの効果測定を下記フローに沿って説明してきております。(下図記載)
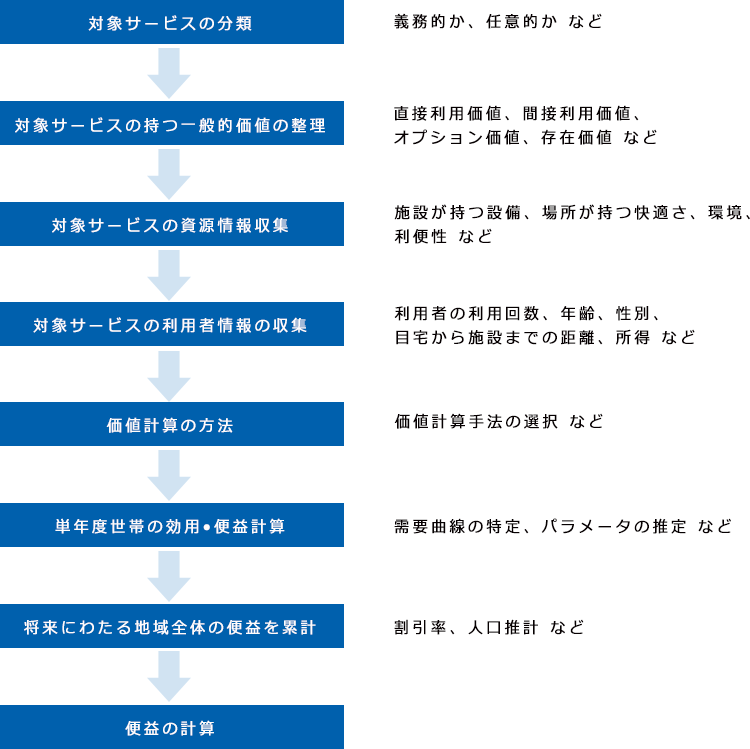 図1:訪問型行政サービスにおける効果測定フロー
図1:訪問型行政サービスにおける効果測定フロー
回帰分析
潜在クラス分析によってセグメント化されたサンプルについて、どのような属性が選択行動に影響を及ぼすのか?を把握するため、選択行動の推計に入る前の準備作業を進めています。
前回のコラムで、相関と「標準化」についての説明を行い、いよいよ核心をつきたい所ではありますが、分析手法として「ロジスティク回帰分析」を用いるため、予め、「回帰分析」の準備が必要になります。回帰分析は、ご存知の方が多いかもしれませんが、「機械学習」を行う上で欠かせない知識です。以前(※1)、統計分析ソフトウェア「R」の統合開発環境「R studio」に用意されているiris(アイリス;あやめ)というデータセットを紹介しましたが、今回も、そのデータを使ってお話しいたします。
Irisは、以下(表1)のようなデータセットになっています。表では冒頭の15行だけを表示していますが、表示されていない135行のデータがあり、計150行です。あやめの「萼(がく):がく」(※2)と「花びら:花弁」を調査したデータになります。
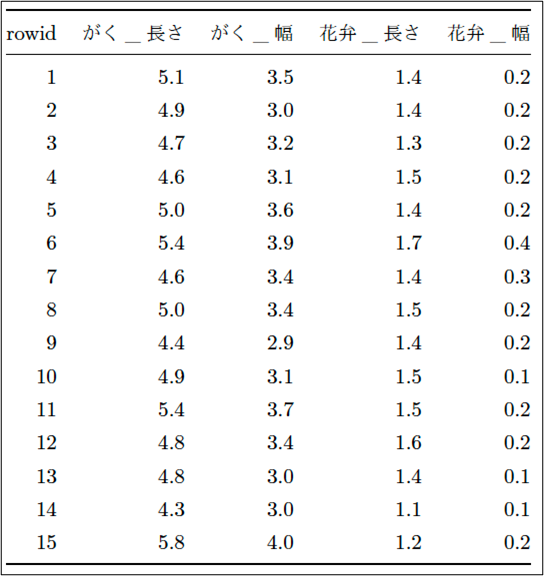 表1:Iris
表1:Iris
今回、上記表1のデータセットを使ってやってみたいことは、「がく_長さ」というあやめの特徴を、他の特徴、すなわち、「がく_幅」・「花弁_長さ」・「花弁_幅」で説明することが可能か?ということです。説明とは、また曖昧な言い回しですが、要は、説明される側の「がく_長さ」をその他3つ(1つでも2つでも良いのですが)のデータの組み合わせで表現できないか?つまり、「がく_長さ」=「がく_幅」 +「 花弁_長さ」 +「 花弁_幅」のような計算式で表せないか?ということなのです。
ただ、それぞれ150行(個)もあるデータのため、単純な足し算の計算式はありません。すなわち、ベクトルです。この場合のベクトルとは、数値の集まり・集合を指します。集合と言っても、それぞれ無秩序なデータの集まりではなくて、上記4つのデータ(それぞれ、150個ありますが)のポジション・位置は決まっています。
このようなデータ群ですが、まずは、4つのデータの関係性を確認してみます。既に、この手の作業は「相関係数」ということで、分析手法を予習しています。また、今回、データ単位はミリで揃っていますので、特に基準化などは考慮しなくても差し支えないでしょう。相関係数は、下記表2のとおりです。行と列に同じ名称が並んでいますが、自分自身どうしの相関は1になるので、表示を省略してあります。
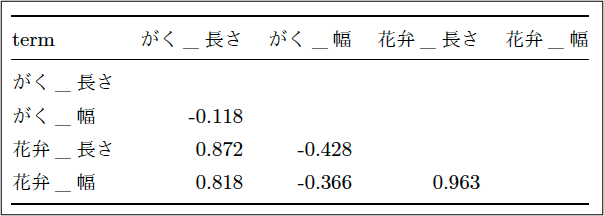 表2:相関係数
表2:相関係数
「がく_長さ」とその他変数との関係ですが、表2列目を眺めていただくと、「がく_幅」とは負の相関(-0.118)があるようです。ただし、その程度はあまり大きく無い。他方で、「花弁_長さ」や「花弁_幅」とは、0.8以上の大きな正の相関が見られます。どうやら「がく_長さ」は「花弁」と強い相関がある。すなわち、「がくの長さは、ある程度花弁で説明できる」ということになりましょう。花弁の2つはどちらも説明力がありそうですが、取り敢えず、相関係数の高い「花弁_長さ」と「花弁_幅」を、別々に使って回帰分析してみましょう。
分析結果~最小二乗法
早速、統計ソフトを使って実行してみましょう。回帰分析の方法は幾つかあると思うのですが、今回は「最小二乗法」を用います。何を「最小」にするのかと言いますと、「誤差の二乗の和」を最小にすることで、最もそれらしい関係式を求めます。誤差=残差というのは、「がく_長さ」と「花弁_長さ」データの1行目を見ていただくと、(5.1 – 3.5)になります。このような誤差が150組計算されます。それらの中にはマイナスもありますので、2乗して、足して・・、ということを行います。そして、これら150組の「誤差の二乗の和」を最小にするような「直線の傾き」を求めます。
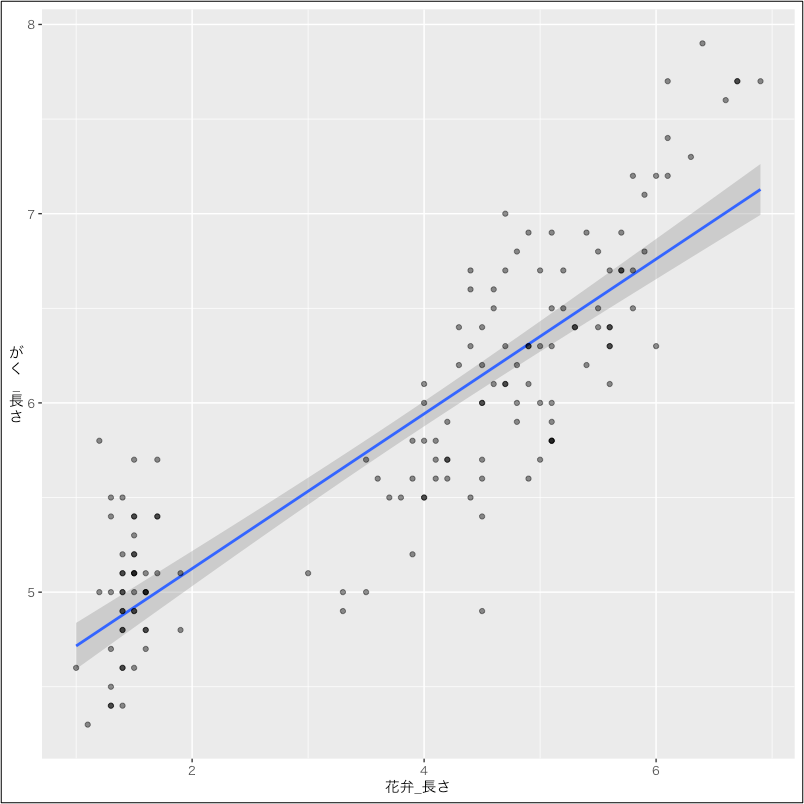 図1:散布図
図1:散布図
上記図1をご覧下さい。縦軸に「がく_長さ」、横軸に「花弁_長さ」が取られています。各点は、実際のデータ、つまり、「がく_長さ」と「花弁_長さ」の関係をプロットしたものになります。「散布図」とも呼ばれます。150の点が表記されています。それらの点を貫いて直線が引かれています。この直線の傾きが求めたかったものですが、凡そ0.4と計算されています。
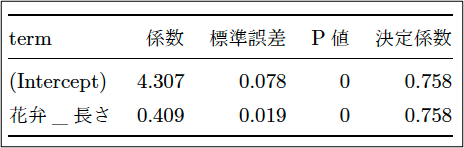 表3:集計結果
表3:集計結果
計算結果は、上記表3になります。2列目の「係数」というのは、正に求めたかった直線の傾きになります。なお、(Intercept)とあるのは、Y軸上の切片です。中学校の一次関数で習った記憶が有ります。「花弁_長さ」の係数が0.409ですから、花弁の長さを0.4倍して、切片4.3を足しておけば、がくの長さを計算できるようになる、という解釈でしょうか。
ただ、図1を見ると、直線の上下に点が結構散らばっているため、正確な関係式が推計できた訳でも無さそうです。どれくらいの説明力が得られたか?それを表すのが四列目にある「決定係数」です。ここからの説明は込み入っているため、次回以降で。
(以上)
コラムニスト
公共事業本部 ソリューションストラテジスト 松村 俊英
参考
- ※1コラム「デジタル社会形成に向けて 第2章(11)~自治体DXの先に~」を参照。
- ※2萼(がく)
植物の花を構成する組織で、花を保護する働きを持つ。
関連コラム
- デジタル社会形成に向けて 第2章(1)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(2)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(3)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(4)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(5)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(6)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(7)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(8)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(9)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(10)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(11)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(12)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(13)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(14)~自治体DXの先に~
- デジタル社会形成に向けて 第2章(15)~自治体DXの先に~
- 「データ分析を考える」コラム一覧に戻る
